精品解析：2022年新高考天津数学高考真题（解析版）（www.ximiyu.com）.docx

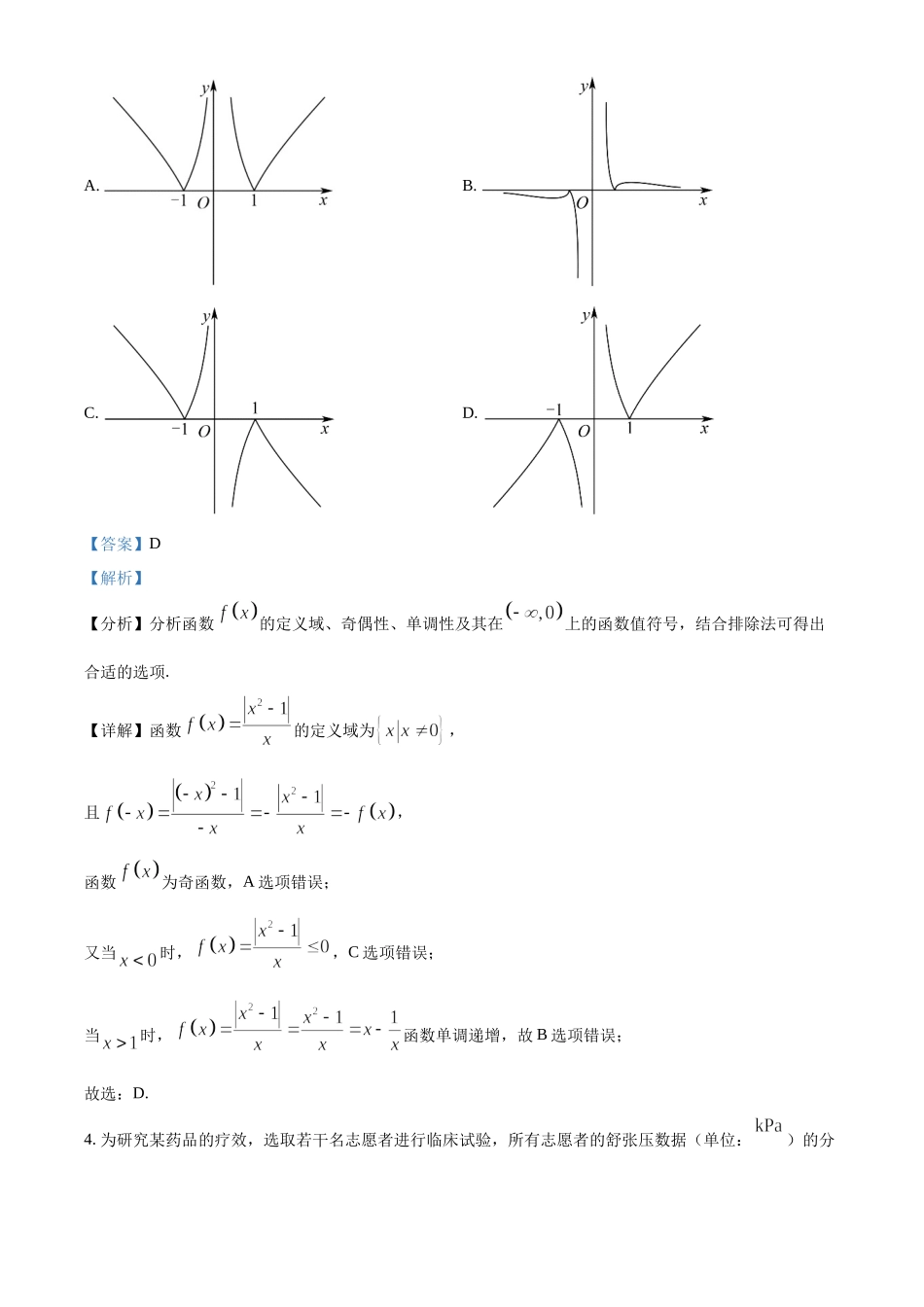
2022年普通高等学校招生全国统一考试数学（天津卷）2022．06． 一、选择题：本题共9小题，每小题5分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 设全集，集合，则（ ） A. B. C. D. 【答案】A 【解析】 【分析】先求出，再根据交集的定义可求. 【详解】，故， 故选：A. 2. “为整数”是“为整数”的（ ） A. 充分不必要 B. 必要不充分 C. 充分必要 D. 既不充分也不必要 【答案】A 【解析】 【分析】依据充分不必要条件的定义去判定“为整数”与“为整数”的逻辑关系即可. 【详解】由题意，若为整数，则为整数，故充分性成立； 当时，整数，但不为整数，故必要性不成立； 所以“为整数”是“为整数”的充分不必要条件. 故选：A. 3. 函数的图像为（ ） A. B. C. D. 【答案】D 【解析】 【分析】分析函数的定义域、奇偶性、单调性及其在上的函数值符号，结合排除法可得出合适的选项. 【详解】函数的定义域为， 且， 函数为奇函数，A选项错误； 又当时，，C选项错误； 当时，函数单调递增，故B选项错误； 故选：D. 4. 为研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：）的分组区间为，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组，右图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为（ ） A. 8 B. 12 C. 16 D. 18 【答案】B 【解析】 【分析】结合已知条件和频率分布直方图求出志愿者的总人数，进而求出第三组的总人数，从而可以求得结果. 【详解】志愿者的总人数为＝50， 所以第三组人数为50×0.36＝18， 有疗效的人数为18－6＝12． 故选：B. 5. 已知，，，则（ ） A. B. C. D. 【答案】C 【解析】 【分析】利用幂函数、对数函数的单调性结合中间值法可得出、、的大小关系. 【详解】因为，故. 故答案为：C. 6. 化简的值为（ ） A. 1 B. 2 C. 4 D. 6 【答案】B 【解析】 【分析】根据对数的性质可求代数式的值. 详解】原式 ， 故选：B 7. 已知抛物线分别是双曲线的左、右焦点，抛物线的准线过双曲线的左焦点，与双曲线的渐近线交于点A，若，则双曲线的标准方程为（ ） A. B. C. D. 【答案】C 【解析】 【分析】由已知可得出的值，求出点的坐标，分析可得，由此可得出关于、、的方程组，解出这三个量的值，即可得出双曲线的标准方程. 【详解】抛物线的准线方程为，则，则、， 不妨设点为第二象限内的点，联立，可得，即点， 因为且，则为等腰直角三角形， 且，即，可得， 所以，，解得，因此，双曲线的标准方程为. 故选：C. 8. 如图，“十字歇山”是由两个直三棱柱重叠后的景象，重叠后的底面为正方形，直三棱柱的底面是顶角为，腰为3的等腰三角形，则该几何体的体积为（ ） A. 23 B. 24 C. 26 D. 27 【答案】D 【解析】 【分析】作出几何体直观图，由题意结合几何体体积公式即可得组合体的体积. 【详解】该几何体由直三棱柱及直三棱柱组成，作于M，如图， 因为，所以， 因为重叠后的底面为正方形，所以, 在直棱柱中，平面BHC，则, 由可得平面， 设重叠后的EG与交点为 则 则该几何体的体积为. 故选：D. 9. 已知，关于该函数有下列四个说法： ①最小正周期为； ②在上单调递增； ③当时，的取值范围为； ④的图象可由的图象向左平移个单位长度得到． 以上四个说法中，正确的个数为（ ） A. B. C. D. 【答案】A 【解析】 【分析】根据三角函数的图象与性质，以及变换法则即可判断各说法的真假． 【详解】因为，所以的最小正周期为，①不正确； 令，而在上递增，所以在上单调递增，②正确；因为，，所以，③不正确； 由于，所以的图象可由的图象向右平移个单位长度得到，④不正确． 故选：A． 第II卷 二、填空题：本大题共6小题，每小题5分，共30分．试题中包含两个空的，答对1个的给3分，全部答对的给5分． 10. 已知是虚数单位，化简的结果为_______． 【答案】## 【解析】 【分析】根据复数代数形式的运算法则即可解出． 【详解】． 故答案为：． 11. 的展开式中的常数项为______. 【答案】 【解析】 【分析】由题意结合二项式定理可得的展开式的通项为，令，代入即可得解. 【详解】由题意的展开式的通项为， 令即，则， 所以的展开式中的常数项为. 故答案为：. 【点睛】本题考查了二项式定理的应用，考查了运算求解能力，属于基础题. 12. 若直线与圆相交所得的弦长为，则_____． 【答案】 【解析】 【分析】计算出圆心到直线的距离，利用勾股定理可得出关于的等式，即可解得的值. 【详解】圆的圆心坐标为，半径为， 圆心到直线的距离为， 由勾股定理可得，因为，解得. 故答案为：. 13. 52张扑克牌，没有大小王，无放回地抽取两次，则两次都抽到A的概率为____________；已知第一次抽到的是A，则第二次抽取A的概率为____________ 【答案】 ①. ②. 【解析】 【分析】由题意结合概率的乘法公式可得两次都抽到A的概率，再由条件概率的公式即可求得在第一次抽到A的条件下，第二次抽到A的概率. 【详解】由题意，设第一次抽到A的事件为B,第二次抽到A的事件为C, 则. 故答案为：；. 14. 在中，，D是AC中点，，试用表示为___________，若，则的最大值为____________ 【答案】 ①. ②. 【解析】 【分析】法一：根据向量的减法以及向量的数乘即可表示出，以为基底，表示出，由可得，再根据向量夹角公式以及基本不等式即可求出． 法二：以点为原点建立平面直角坐标系，设，由可得点的轨迹为以为圆心，以为半径的圆，方程为，即可根据几何性质可知，当且仅当与相切时，最大，即求出． 【详解】方法一： ，， ，当且仅当时取等号，而，所以． 故答案为：；． 方法二：如图所示，建立坐标系： ，， ，所以点的轨迹是以为圆心，以为半径的圆，当且仅当与相切时，最大，此时． 故答案为：；． 15. 设，对任意实数x，记．若至少有3个零点，则实数取值范围为______. 【答案】 【解析】 【分析】设，，分析可知函数至少有一个零点，可得出，求出的取值范围，然后对实数的取值范围进行分类讨论，根据题意可得出关于实数的不等式，综合可求得实数的取值范围. 【详解】设，，由可得. 要使得函数至少有个零点，则函数至少有一个零点，则， 解得或. ①当时，，作出函数、的图象如下图所示： 此时函数只有两个零点，不合乎题意； ②当时，设函数的两个零点分别为、， 要使得函数至少有个零点，则， 所以，，解得； ③当时，，作出函数、的图象如下图所示： 由图可知，函数的零点个数为，合乎题意； ④当时，设函数的两个零点分别为、， 要使得函数至少有个零点，则， 可得，解得，此时. 综上所述，实数的取值范围是. 故答案为：. 【点睛】方法点睛：已知函数有零点（方程有根）求参数值（取值范围）常用的方法： （1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决； （3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解. 三、解答题：本大题共5小题，共75分，解答应写出文字说明，证明过程或演算步骤． 16. 在中，角A、B、C的对边分别为a，b，c.已知. （1）求的值； （2）求的值； （3）求的值. 【答案】（1） （2） （3） 【解析】 【分析】（1）根据余弦定理以及解方程组即可求出； （2）由（1）可求出，再根据正弦定理即可解出； （3）先根据二倍角公式求出，再根据两角差的正弦公式即可求出． 【小问1详解】 因为，即，而，代入得，解得：． 【小问2详解】 由（1）可求出，而，所以，又，所以． 【小问3详解】 因为，所以，故，又， 所以，，而，所以， 故． 17. 直三棱柱中，，D为的中点，E为的中点，F为的中点． （1）求证：平面； （2）求直线与平面所成角的正弦值； （3）求平面与平面所成二面角的余弦值． 【答案】（1）证明见解析 （2） （3） 【解析】 【分析】（1）以点为坐标原点，、、所在直线分别为、、轴建立空间直角坐标系，利用空间向量法可证得结论成立； （2）利用空间向量法可求得直线与平面夹角的正弦值； （3）利用空间向量法可求得平面与平面夹角的余弦值. 【小问1详解】 证明：在直三棱柱中，平面，且，则 以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系， 则、、、、、、、、，则， 易知平面的一个法向量为，则，故， 平面，故平面. 【小问2详解】 解：，，， 设平面的法向量为，则， 取，可得，. 因此，直线与平面夹角的正弦值为. 【小问3详解】 解：，， 设平面的法向量为，则， 取，可得，则， 因此，平面与平面夹角的余弦值为. 18. 设是等差数列，是等比数列，且． （1）求与的通项公式； （2）设的前n项和为，求证：； （3）求． 【答案】（1） （2）证明见解析 （3） 【解析】 【分析】（1）利用等差等比数列的通项公式进行基本量运算即可得解； （2）由等比数列的性质及通项与前n项和的关系结合分析法即可得证； （3）先求得，进而由并项求和可得，再结合错位相减法可得解. 【小问1详解】 设公差为d，公比为，则， 由可得（舍去）， 所以； 【小问2详解】 证明：因为所以要证， 即证，即证， 即证， 而显然成立，所以； 【小问3详解】 因为 ， 所以 ， 设 所以， 则， 作差得 ， 所以， 所以. 19. 椭圆的右焦点为F、右顶点为A，上顶点为B，且满足． （1）求椭圆的离心率； （2）直线l与椭圆有唯一公共点M，与y轴相交于N（N异于M）．记O为坐标原点，若，且的面积为，求椭圆的标准方程． 【答案】（1） （2） 【解析】 【分析】（1）根据已知条件可得出关于、的等量关系，由此可求得该椭圆的离心率的值； （2）由（1）可知椭圆的方程为，设直线的方程为，将直线的方程与椭圆方程联立，由可得出，求出点的坐标，利用三角形的面积公式以及已知条件可求得的值，即可得出椭圆的方程. 【小问1详解】 解：， 离心率为. 【小问2详解】 解：由（1）可知椭圆的方程为， 易知直线的斜率存在，设直线的方程为， 联立得， 由，① ，， 由可得，② 由可得，③ 联立①②③可得，，，故椭圆的标准方程为． 20. 已知，函数 （1）求函数在处的切线方程； （2）若和有公共点， （i）当时，求的取值范围； （ii）求证：． 【答案】（1） （2）（i）；（ii）证明见解析 【解析】 【分析】（1）求出可求切线方程； （2）（i）当时，曲线和有公共点即为在上有零点，求导后分类讨论结合零点存在定理可求. （ii）曲线和有公共点即，利用点到直线的距离得到，利用导数可证，从而可得不等式成立. 【小问1详解】 ，故，而， 曲线在点处的切线方程为即. 【小问2详解】 （i）当时， 因为曲线和有公共点，故有解， 设，故，故在上有解， 设，故在上有零点， 而， 若，则恒成立，此时在上无零点， 若，则在上恒成立，故在上为增函数， 而，，故在上无零点， 故， 设，则， 故在上为增函数， 而，， 故在上存在唯一零点， 且时，；时，； 故时，；时，； 所以在上为减函数，在上为增函数， 故， 因为在上有零点，故，故， 而，故即， 设，则， 故在上为增函数， 而，故. （ii）因为曲线和有公共点， 所以有解，其中， 若，则，该式不成立，故. 故，考虑直线， 表示原点与直线上的动点之间的距离， 故，所以， 下证：对任意，总有， 证明：当时，有，故成立. 当时，即证， 设，则（不恒为零）， 故在上减函数，故即成立. 综上，成立. 下证：当时，恒成立， ，则， 故在上为增函数，故即恒成立. 下证：在上恒成立，即证：， 即证：，即证：， 而，故成立. 故，即成立. 【点睛】思路点睛：导数背景下零点问题，注意利用函数的单调性结合零点存在定理来处理，而多变量的不等式的成立问题，注意从几何意义取构建不等式关系，再利用分析法来证明目标不等式.