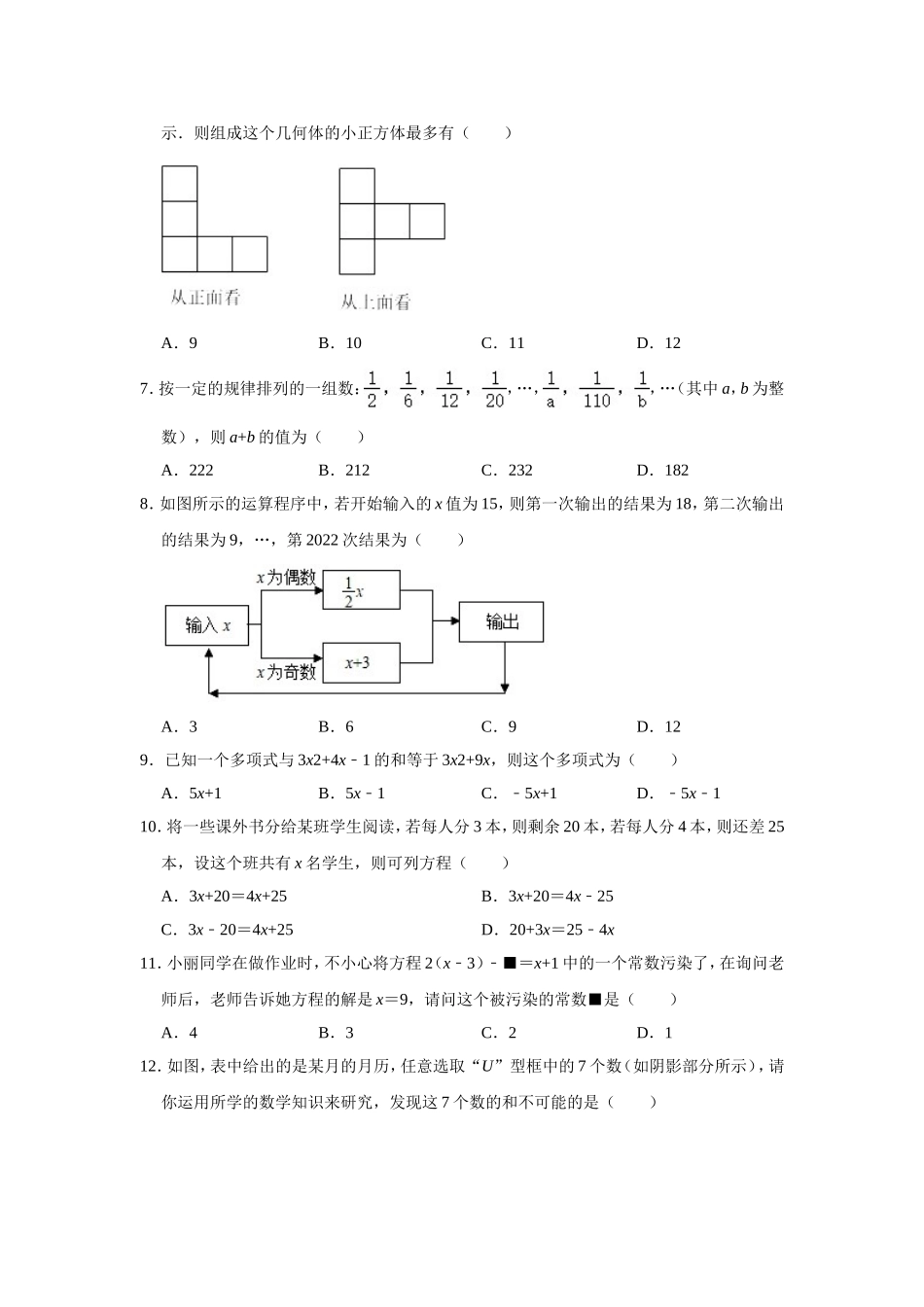
2021-2022学年山东省淄博市桓台县六年级(上)期末数学试卷(五四学制)一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分,在每小题所给出的四个选项中,只有一项是符合题目要求的.)1.如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“负”相对的面上的汉字是()A.强B.课C.提D.质2.运用等式性质进行的变形,不正确的是()A.如果a=b,那么a﹣c=b﹣cB.如果a﹣c=b﹣c,那么a=bC.如果ac2=bc2,那么a=bD.如果a(c2+1)=b(c2+1),那么a=b3.有长为L的篱笆,利用它和房屋的一面墙围成如图形状的长方形园子,园子的宽为t,则所围成的园子面积为()A.(L﹣)tB.(L﹣t)tC.(﹣t)tD.(L﹣2t)t4.某公司今年2月份的利润为x万元,3月份比2月份减少7%,4月份比3月份增加了8%,则该公司4月份的利润为()(单位:万元)A.(x﹣7%)(x+8%)B.(x﹣7%+8%)C.(1﹣7%+8%)xD.(1﹣7%)(1+8%)x5.如果a﹣b>0,且a+b<0,那么一定正确的是()A.a为正数,且|b|>|a|B.a为正数,且|b|<|a|C.b为负数,且|b|>|a|D.b为负数,且|b|<|a|6.一个几何体是由一些大小相同的小正方体组成的,其从上面与从正面看到的形状如图所示.则组成这个几何体的小正方体最多有()A.9B.10C.11D.127.按一定的规律排列的一组数:,…,,…(其中a,b为整数),则a+b的值为()A.222B.212C.232D.1828.如图所示的运算程序中,若开始输入的x值为15,则第一次输出的结果为18,第二次输出的结果为9,…,第2022次结果为()A.3B.6C.9D.129.已知一个多项式与3x2+4x﹣1的和等于3x2+9x,则这个多项式为()A.5x+1B.5x﹣1C.﹣5x+1D.﹣5x﹣110.将一些课外书分给某班学生阅读,若每人分3本,则剩余20本,若每人分4本,则还差25本,设这个班共有x名学生,则可列方程()A.3x+20=4x+25B.3x+20=4x﹣25C.3x﹣20=4x+25D.20+3x=25﹣4x11.小丽同学在做作业时,不小心将方程2(x﹣3)﹣■=x+1中的一个常数污染了,在询问老师后,老师告诉她方程的解是x=9,请问这个被污染的常数■是()A.4B.3C.2D.112.如图,表中给出的是某月的月历,任意选取“U”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()A.70B.78C.77D.105二、填空题(本大题共5个小题,每小题4分,共20分。请直接填写最后结果.)13.若2xmy与x3y是同类项...