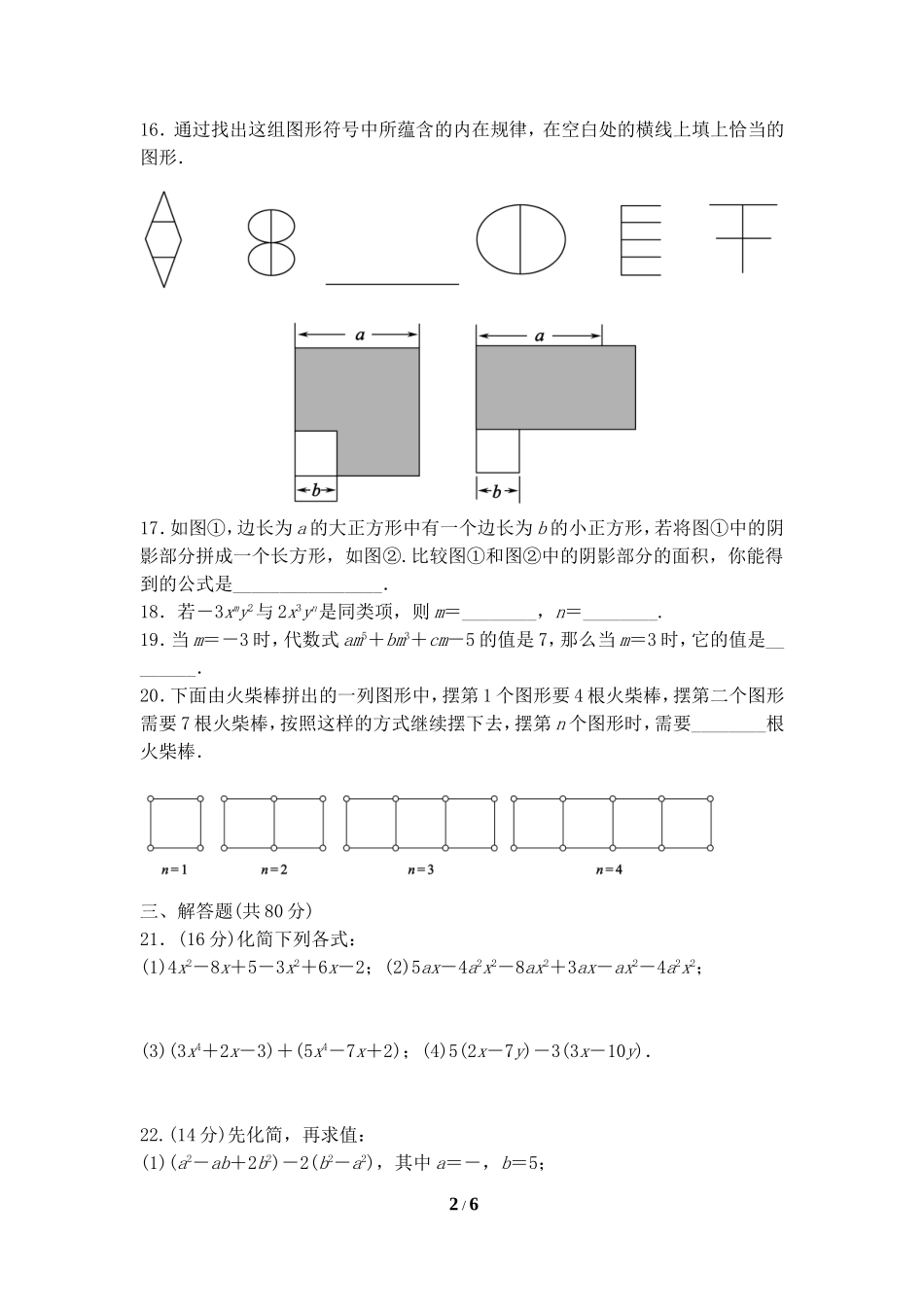
第三章评估测试卷(测试时间:120分钟测试总分:150分)一、选择题(每小题3分,共30分)1.用语言叙述-2表示的数量关系中,表达不正确的是()A.比a的倒数小2的数B.比a的倒数大2的数C.a的倒数与2的差D.1除以a的商与2的差2.下列各式中:m,-,x-2,,,,,单项式的个数为()A.5B.4C.3D.23.一个两位数是a,在它左边加上一个数字b变成三位数,则这个三位数用代数式表示为()A.10a+100bB.baC.100baD.100b+a4.下列去括号错误的是()A.3a2-(2a-b+5c)=3a2-2a+b-5cB.5x2+(-2x+y)-(3z-u)=5x2-2x+y-3z+uC.2m2-3(m-1)=2m2-3m-1D.-(2x-y)-(-x2+y2)=-2x+y+x2-y25.合并同类项2mx+1-3mx-2(-mx-2mx+1)的结果是()A.4mxx+1-5mxB.6mx+1+mxC.4mx+1+5mxD.6mx+1-mx6.已知-x+2y=6,则3(x-2y)2-5(x-2y)+6的值是()A.84B.144C.72D.3607.已知A=5a-3b,B=-6a+4b,即A-B等于()A.-a+bB.11a+bC.11a-7bD.-a-7b8.x表示一个两位数,y表示一个三位数,如果把x放在y的左边组成一个五位数那么这个五位数就可以表示为()A.xyB.x+yC.1000x+yD.10x+y9.当代数式x2+4取最小值时,x的值应是()A.0B.-1C.1D.410.已知大家以相同的效率做某件工作,a人做b天可以完工,若增加c人,则完成工作提前的天数为()A.(-b)天B.(-b)天C.(b-)天D.(b-)天二、填空题(每小题4分,共40分)11.用代数式表示:(1)钢笔每支a元,m支钢笔共________元;(2)一本书有a页,小明已阅读b页,还剩________页.12.-+x3的次数是________.13.当x=-时,代数式1-3x2的值是________.14.代数式6a2-7b2+2a2b-3ba2+6b2中没有同类项的是________.15.如果|m-3|+(n-2)2=0,那么-5xmyn+7x3y2=________.1/616.通过找出这组图形符号中所蕴含的内在规律,在空白处的横线上填上恰当的图形.17.如图①,边长为a的大正方形中有一个边长为b的小正方形,若将图①中的阴影部分拼成一个长方形,如图②.比较图①和图②中的阴影部分的面积,你能得到的公式是________________.18.若-3xmy2与2x3yn是同类项,则m=________,n=________.19.当m=-3时,代数式am5+bm3+cm-5的值是7,那么当m=3时,它的值是________.20.下面由火柴棒拼出的一列图形中,摆第1个图形要4根火柴棒,摆第二个图形需要7根火柴棒,按照这样的方式继续摆下去,摆第n个图形时,需要________根火柴棒.三、解答题(共80分...