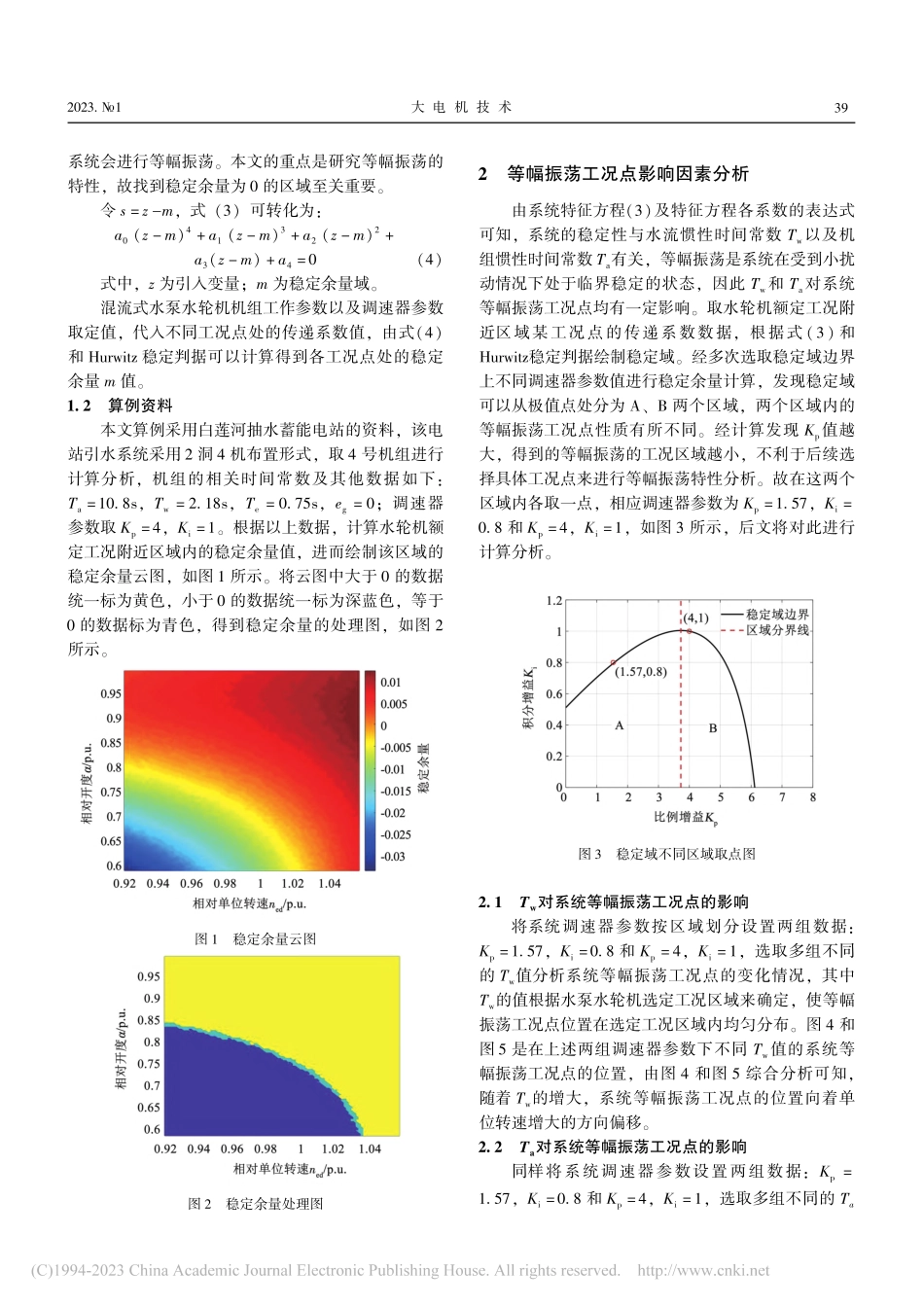
2023.№1大电机技术■■■■■■■■■■■■■■■■■■■■■■■■■■■■水轮机及水泵抽水蓄能机组小波动等幅振荡特性与查看全文彩图工况点的关联规律邵子轩,杨威嘉,廖溢文,李旭东(水资源与水电工程科学国家重点实验室(武汉大学),武汉430072)[摘要]抽水蓄能机组的动态调节稳定性是电站参与电网调峰调频、支撑新能源消纳的关键,而机组在小波动过渡过程工况中的等幅振荡特性,是研究系统稳定性及稳定临界工况的要点。本文采用抽水蓄能机组调节系统的小波动数学模型,运用MATLAB仿真分析工况点的稳定余量,阐释了系统关键时间常数对等幅振荡工况点的影响,揭示了等幅振荡特性与工况点的关联规律。结果表明:水流惯性时间常数Tw的增大使系统等幅振荡工况点的位置向单位转速增大方向移动,机组惯性时间常数Ta的增大使系统等幅振荡工况点的位置向单位转速减小方向移动;随着工况点单位转速的增大,等幅振荡的幅值减小,频率增大;随着工况点开度的增大,等幅振荡的幅值增大,频率减小;Tw对频率的影响呈负相关;Ta对振幅的影响呈负相关。[关键词]抽水蓄能机组;工况点;关键时间常数;等幅振荡;小波动数学模型;MATLAB仿真分析[中图分类号]TK734[文献标志码]A[文章编号]1000⁃3983(2023)01⁃0037⁃07CorrelationLawBetweenSustainedOscillationCharacteristicsandOperatingPointofPumpedStorageUnitsUnderSmallFluctuationSHAOZixuan,YANGWeijia,LIAOYiwen,LIXudong(StateKeyLaboratoryofWaterResourcesandHydropowerEngineeringScience(WuhanUniversity),Wuhan430072,China)Abstract:Dynamicregulationstabilityofpumpedstorageunitisthekeyforpowerstationtoparticipateinpeakloadandfrequencyregulationandsupportnewenergyconsumption,andthesustainedoscillationcharacteristi...