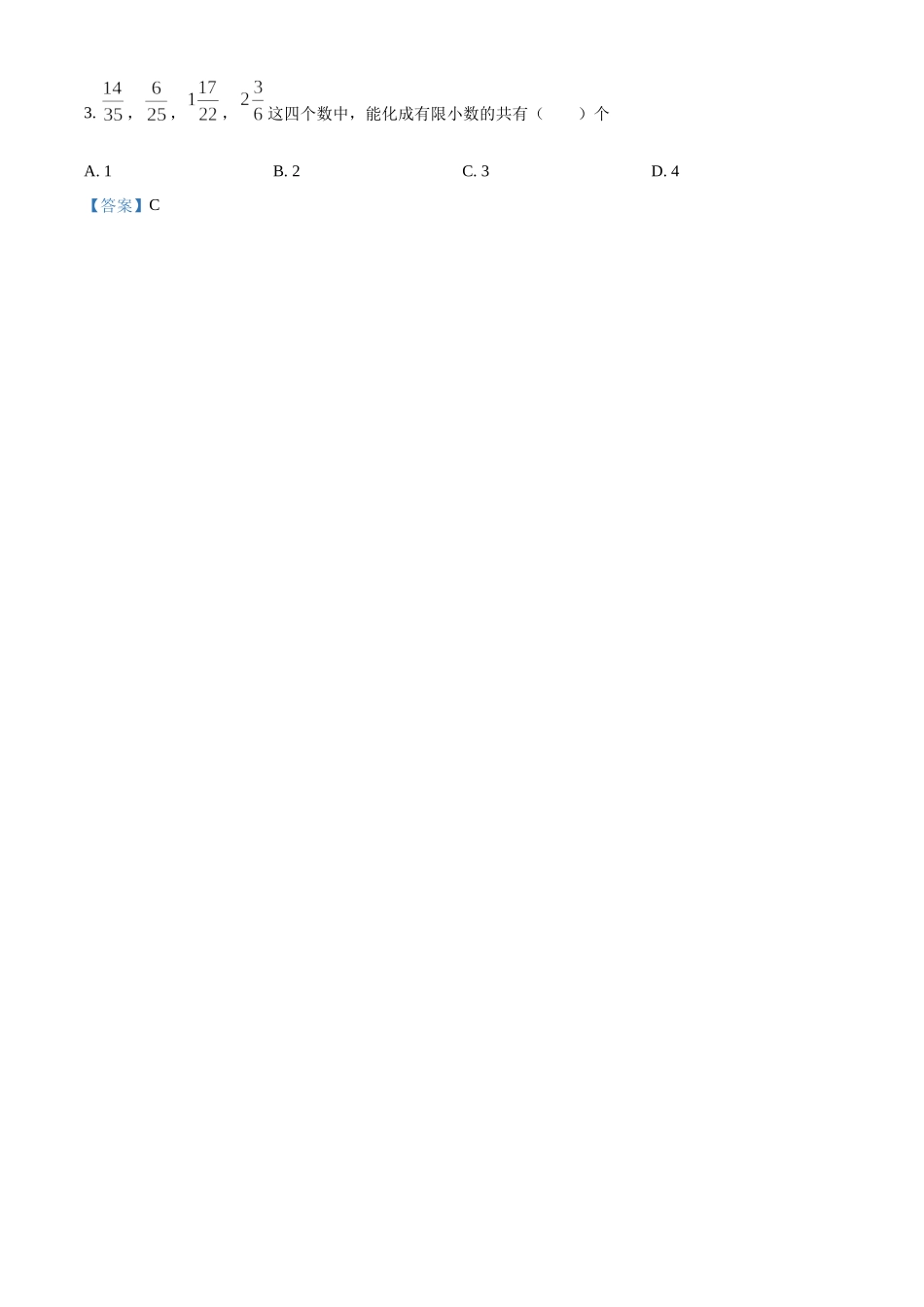
六年级数学学科(考试时间:90分钟,满分:100分)一、选择题(每题3分,满分18分)1.在下列算式中,被除数能被除数整除的是()A.6.3÷3B.6÷3C.3÷6D.33÷6【答案】B【解析】【分析】根据有理数的除法分别计算各选项,即可得出答案.【详解】解:A选项,6.3不是整数,故该选项不符合题意;B选项,6÷3=2,故该选项符合题意;C选项,3÷6=0.5,故该选项不符合题意;D选项,33÷6=5.5,故该选项不符合题意;故选:B.【点睛】本题考查了有理数的除法,掌握若整数a除以非零整数b,商为整数,且余数为零,我们就说a能被b整除是解题的关键.2.分数介于两个相邻的整数之间,这两个整数是()A.3和4B.4和5C.5和6D.6和7【答案】D【解析】【分析】把化成带分数后,看其整数部分找相邻的两个整数.【详解】解:,,分数介于5和6之间故选D.【点睛】本题考查了有理数的大小比较,明确问题中“两个相邻整数”的含义是解题关键.3.,,,这四个数中,能化成有限小数的共有()个A.1B.2C.3D.4【答案】C【解析】【分析】先看分数是否为最简分数,如果不是先进行化最简分数,如果分母中除了2和5以外,不再含有其他的质因数,这个分数就能化成有限小数,如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数,据此进行排除选项即可.【详解】解:化成最简分数为,分母中含有质因数5,能化成有限小数;是最简分数,分母中只含有质因数5,能化成有限小数;是最简分数,分母中含有质因数2和11,不能化成有限小数;化成最简分数是,分母中只含有质因数2,能化成有限小数;所以能化成有限小数的有3个,故C正确;故选:C.【点睛】本题主要考查分数化小数,熟练掌握分数化小数是解题的关键.4.下列说法正确的是()A.素数只有自己一个因数B.素数不一定都是奇数C.在正整数中,除了素数就是合数D.互素的两数没有公因数【答案】B【解析】【分析】根据素数的定义,素数,指的是“大于1的整数中,只能被1和这个数本身整除的数”,逐项分析判断即可.【详解】解:A.素数有1和自己两个因数,故该选项不正确,不符合题意;B.素数不一定都是奇数,例如2,故该选项正确,符合题意;C.在正整数中,1不是素数也不是合数,故该选项不正确,不符合题意.D.互素的两数有公因数1,故该选项不正确,不符合题意;故选:B.【点睛】本题考查素数与合数的定义,掌握素数的定义是解题的关键.5.甲数=2×2×3×5,乙数=2×3×3×7,它们的最小公倍数是()A.6B.36C.210D.1260【答案...