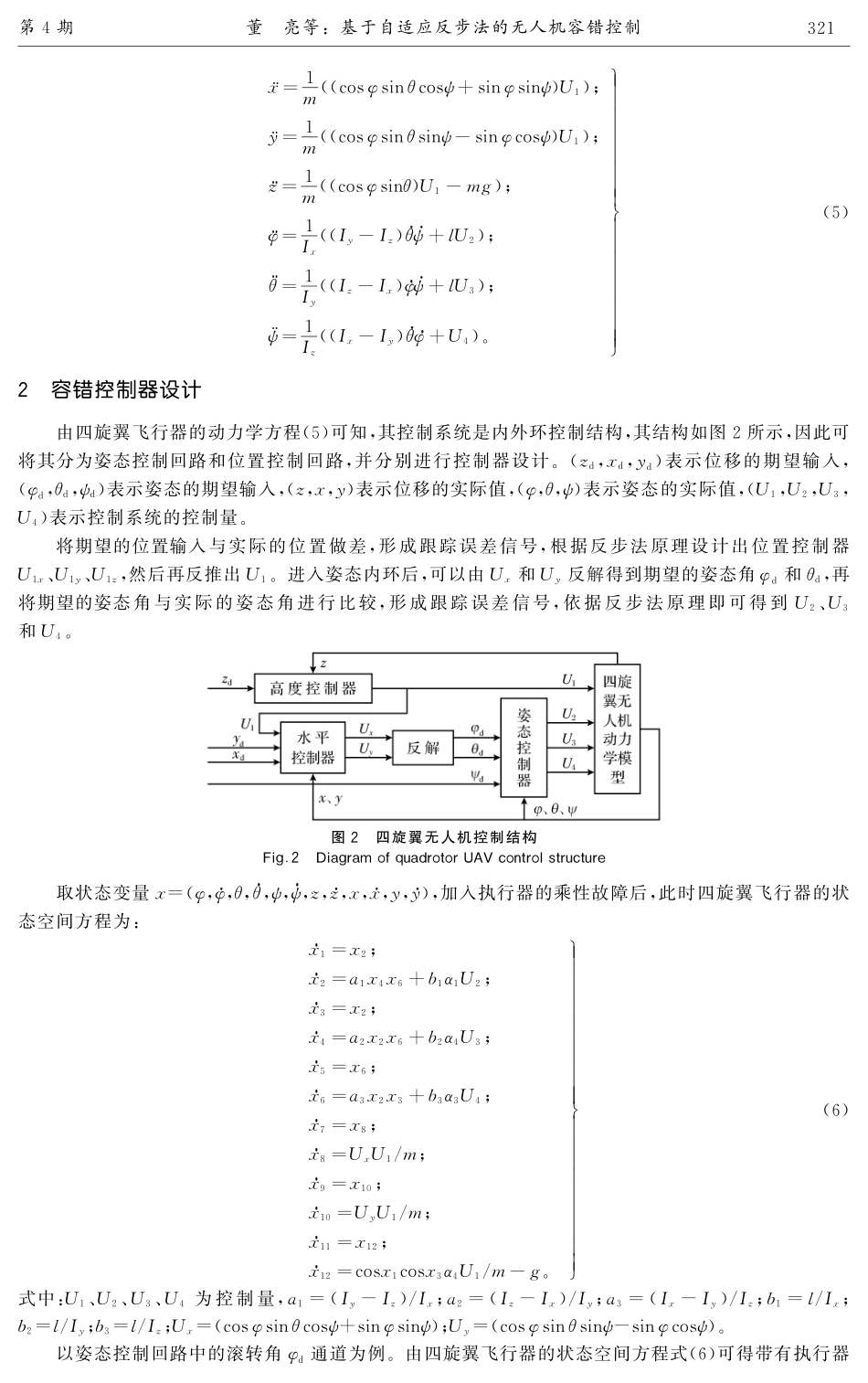
收稿日期:20221022基金项目:中国博士后科学基金资助项目(2020M680979);辽宁省自然科学基金资助项目(2021-BS-281)。作者简介:董亮(1980),男,辽宁沈阳人,副教授,博士。第35卷第4期2023年8月沈阳大学学报(自然科学版)JournalofShenyangUniversity(NaturalScience)Vol.35,No.4Aug.2023文章编号:2095-5456(2023)04-0319-07基于自适应反步法的无人机容错控制董亮,丁甜甜,霍焱(沈阳大学信息工程学院,辽宁沈阳110044)摘要:针对四旋翼飞行器控制系统执行器发生乘性故障的问题,基于自适应反步法设计了容错控制器。针对“X”型飞行器进行动力学建模,将四旋翼飞行器的数学模型分为姿态角通道和高度通道。对这2个通道分别建立一系列自适应律来在线估计故障因子,以补偿执行器故障给系统带来的影响,实现无人机系统的容错控制。通过MATLAB仿真实验,验证了这种基于反步法的自适应容错控制的有效性。关键词:四旋翼飞行器;反步法;自适应控制;容错控制;执行器故障中图分类号:TP277文献标志码:AFault-TolerantControlofAircraftBasedonAdaptiveBacksteppingDONGLiang,DINGTiantian,HUOYan(SchoolofInformationEngineering,ShenyangUniversity,Shenyang110044,China)Abstract:Afault-tolerantcontrollerwasdesignedbasedontheadaptivebacksteppingmethodforaircraftsystemswithmultiplicityactuatorfailures.Thedynamicsmodelingofthe“X”aircraftwascarriedout,andthemathematicalmodelofthequadcopterwasdividedintoattitudeanglechannelandaltitudechannel.Forthesetwochannels,aseriesofadaptivelawswereestablishedtoestimatethefaultfactoronlinetocompensatefortheimpactofactuatorfailureonthesystemandrealizethefault-tolerantcontroloftheUAVsystem.Withoutknowingtheactuatorfaultboundaryinformation,theresultingclosed-loopsystemwasgraduallystabilized.ThroughMATLABsimulationexperiments,theeffectivenessofthisadaptivefault-tolerantcontrolbasedonbacksteppingmethodwasverified.Keywords:quadcopter;backstepping;adaptivecontrol;fault-tolerantcontrol;actuatorfailure四旋翼飞行器的质量轻、体积小、机动性强,十分便于携带,在日常生活中的应用越来越广泛,为我们的社会带来了很多方便。实际应用中,随机扰动和实际环境的变化会引发执行器故障问题,并且它本身是一个拥有多输入和多输出的强耦合、非线性复杂被控对象,因此,为实现对飞行器的精确控...