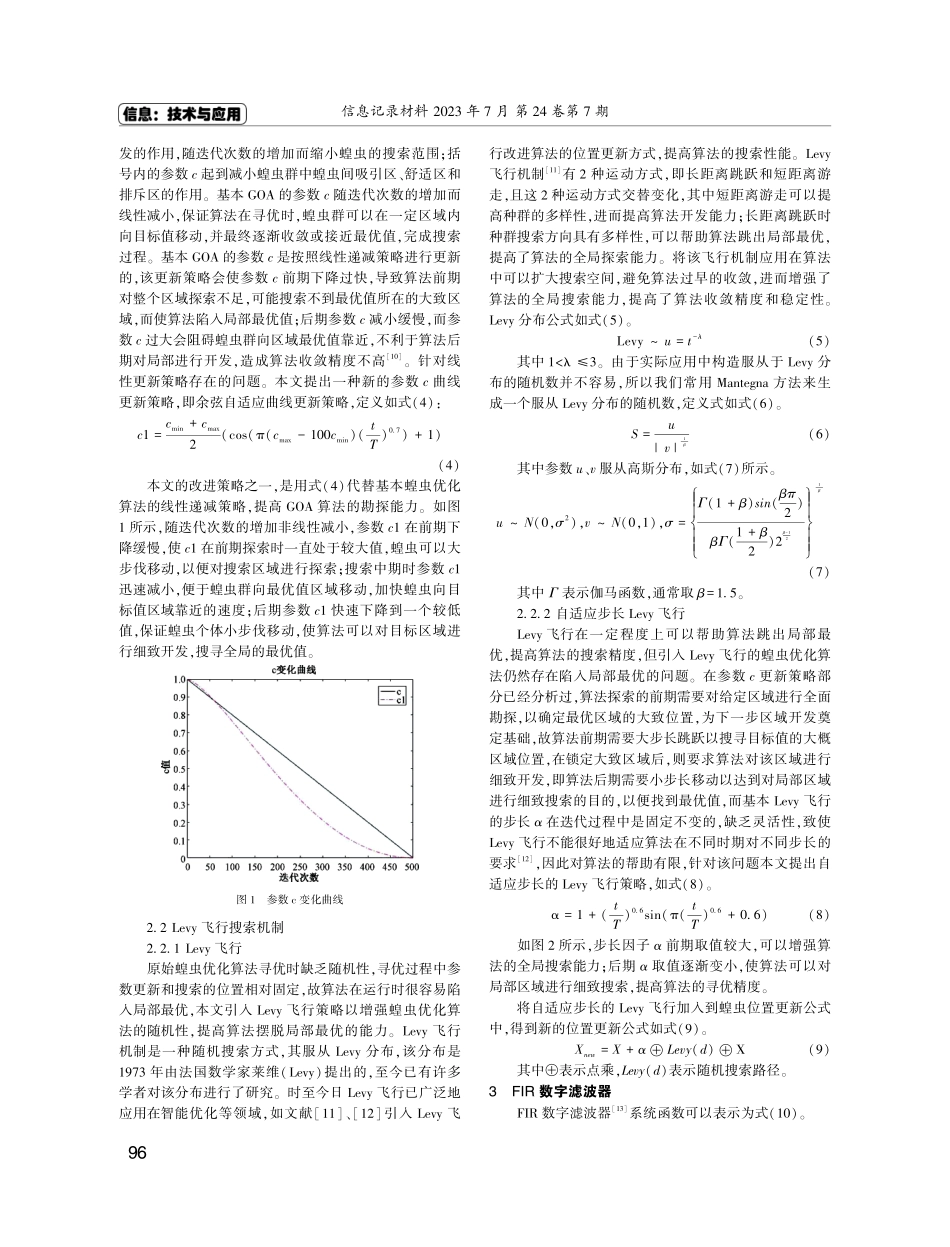
信息记录材料2023年7月第24卷第7期基于改进蝗虫优化算法的FIR滤波器设计何成港,刘国巍(安徽理工大学电气与信息工程学院安徽淮南232000)【摘要】针对蝗虫优化算法(GOA)在设计有限脉冲响应(FIR)数字滤波器时易陷入局部最优等问题,引入参数c非线性递减、自适应步长的Levy飞行策略,提出一种改进的蝗虫优化算法(IGOA)并将其应用在FIR数字滤波器设计上。仿真结果表明与原始GOA和粒子群算法(PSO)相比,改进的蝗虫优化算法设计FIR数字滤波器时更加稳定、有效。【关键词】蝗虫优化算法;有限脉冲响应滤波器;参数优化;Levy飞行【中图分类号】TP39【文献标识码】A【文章编号】1009-5624(2023)07-0095-040引言随着数字信息技术的快速发展,数字信号处理技术的发展也受到了广泛的关注,而数字滤波器在数字信号处理系统中起着至关重要的作用,其性能的好坏关系到数字信号处理的效果。从单位脉冲响应长度分类[1],数字滤波器可分为有限长单位脉冲滤波器(FIR)、无限长单位脉冲响应滤波器(IIR)。相较于IIR数字滤波器,FIR数字滤波器具有线性相位、稳定、易于实现等优势[1]。正因如此,FIR滤波器在许多工程领域有着广泛的应用价值,如在图像处理、音频处理等领域[2-3]。传统设计FIR滤波器的方法有窗函数法、频率采样法等方法[4],虽然设计出来的滤波器也可以得到不错的效果,但在滤波器通带和阻带中会出现许多小波纹,传统设计方法也存在易陷入局部最优、收敛精度差等问题[5]。为了能够改善FIR数字滤波器性能,众多学者做了大量的探索实验,其中部分学者提出使用智能优化算法来设计FIR数字滤波器,诸如粒子群算法(PSO)[5]、蝗虫优化算法(GOA)[6]等智能算法被用来设计FIR滤波器,这些智能优化算法以数字滤波器系数为变量,在一定的优化准则下,得到一组最优的数字滤波器系数。2017年由SAREMI等[7]提出的蝗虫优化算法(GOA),是一种群体智能优化方法,设计灵感来源于自然界中蝗虫的群集行为,同其他智能优化算法一样,基本GOA也存在易陷入局部最优、收敛精度低的缺点,有些情况下过早收敛无法取得全局最优[8-9],若将GOA直接应用在FIR数字滤波器设计中,其本身存在的缺陷会影响滤波器设计性能和效率,故需要改善GOA算法,以便在设计时可以获得满足要求的数字滤波器。针对原始蝗虫优化算法在应用中存在的不足,众多学者提出了不同的改进策略,如QIN等[8]提出将重力和速度引入GOA中每个蝗虫的更新位置,一定程度上提高了算法收敛速度和精度;李洋州等[9]提出曲线自适应和模拟退火蝗虫优化的改进策略,该方法...