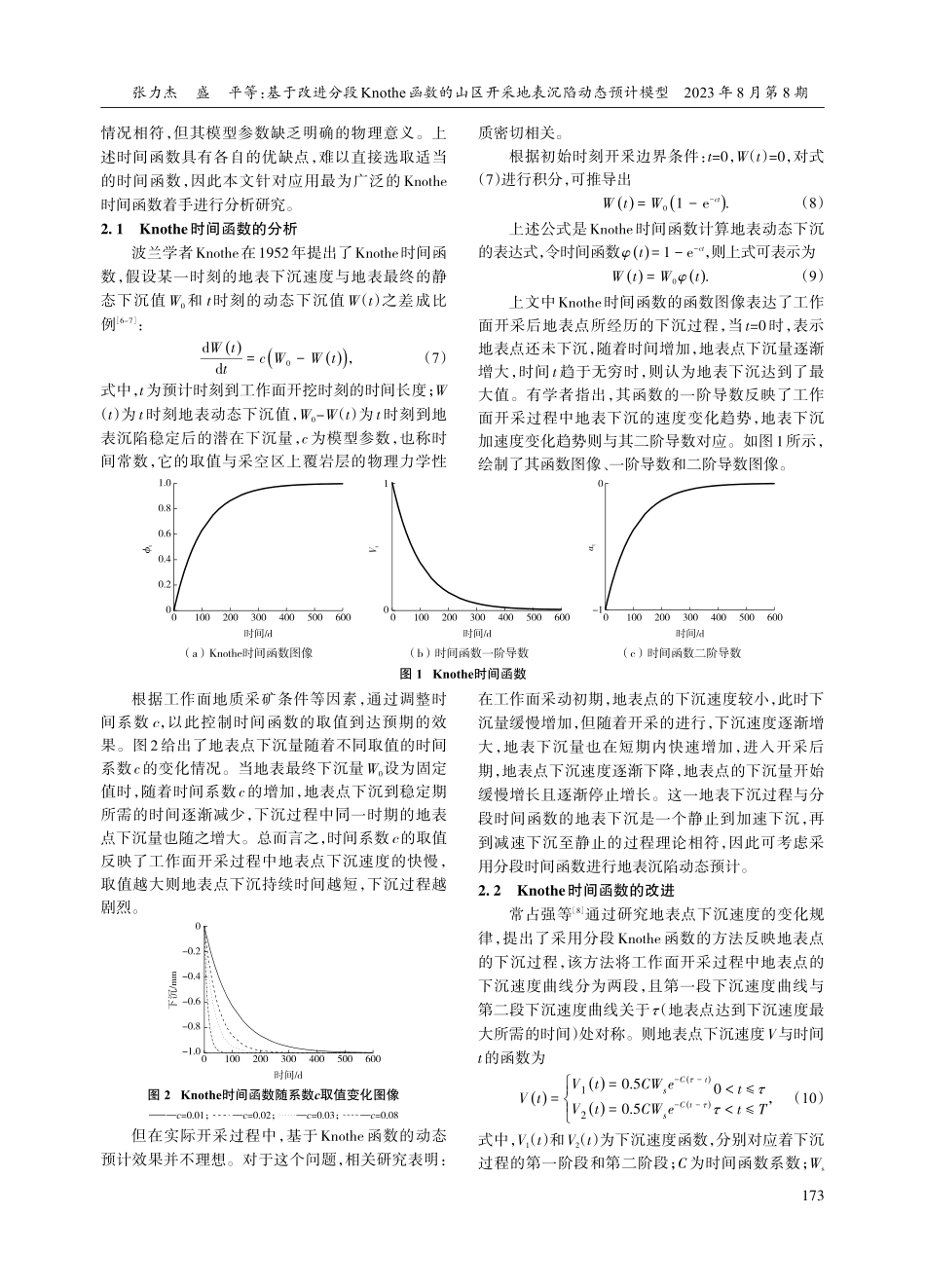
*国家自然科学基金项目(编号:51974292)。张力杰(1986—),男,工程师,250101山东省济南市。基于改进分段Knothe函数的山区开采地表沉陷动态预计模型*张力杰1盛平2郑诚3(1.山东能源集团有限公司;2.中国矿业大学力学与土木工程学院;3.杭州杭港地铁有限公司)摘要复杂地形地貌等因素的影响下,山区地形下煤炭资源地下开采引起的地表移动变形过程相比平原地区对地表建(构)筑物的影响更为严重,因此准确预计山区地形下采动过程中的地表移动变形是保障建(构)筑物安全的重要前提。基于山区开采沉陷滑移模型,建立了基于改进后Knothe时间函数的山区开采地表沉陷动态预计模型,并采用山西某矿3302工作面的实测地表下沉数据验证该模型的实用性与可靠性。结果表明:Knothe函数的预计模型不能很好地反映地表点下沉完整过程;改进后的Knothe函数的预计结果显著改善,各期预计值中误差相对于实测最大下沉值的相对误差最大值为6.56%,模型预计结果与实测下沉数据具有较好的一致性,满足工程需求。关键词山区采动时间函数动态预计开采沉陷DOI:10.3969/j.issn.1674-6082.2023.08.041DynamicPredictionModelofSurfaceSubsidenceinMountainousMiningBasedonSubsectionKnotheFunctionZHANGLijie1SHENGPing2ZHENGCheng3(1.ShandongEnergyGroupCo.,Ltd.;2.CollegeofMechanicsandCivilEngineering,ChinaUniversityofMiningandTechnology;3.HangzhouHangangMetroCo.,Ltd.)AbstractUndertheinfluenceoffactorssuchascomplextopographyandtopography,thesurfacemovementanddeformationprocesscausedbyundergroundminingofcoalresourcesinmountainousterrainisdifferentfromthatinplainareas,andtheimpactonsurfacebuildings(structures)ismoreserious.There⁃fore,accuratepredictionofsurfacemovementanddeformationduringmininginmountainousterrainisanimportantprerequisiteforensuringthesafetyofbuildings(structures).Basedonthesubsidence-slipmodelofmininginmountainousareas,adynamicpredictionmodelofsurfacesubsidenceinmountainousminingbasedontheimprovedKnothetimefunctionwasestablished,andthepracticalityandreliabilityofthemod⁃elwereverifiedbyusingthemeasuredsurfacesubsidencedataofthe3302workingfaceofamineinShanxi.TheresultsshowthatthepredictionmodelbasedontheKnothefunctionhasflawsandcannotreflectthecompletes...