数学（理）卷07-2020年高三数学（理）【名校、地市联考】精选仿真模拟卷（解析版）.pdfVIP免费

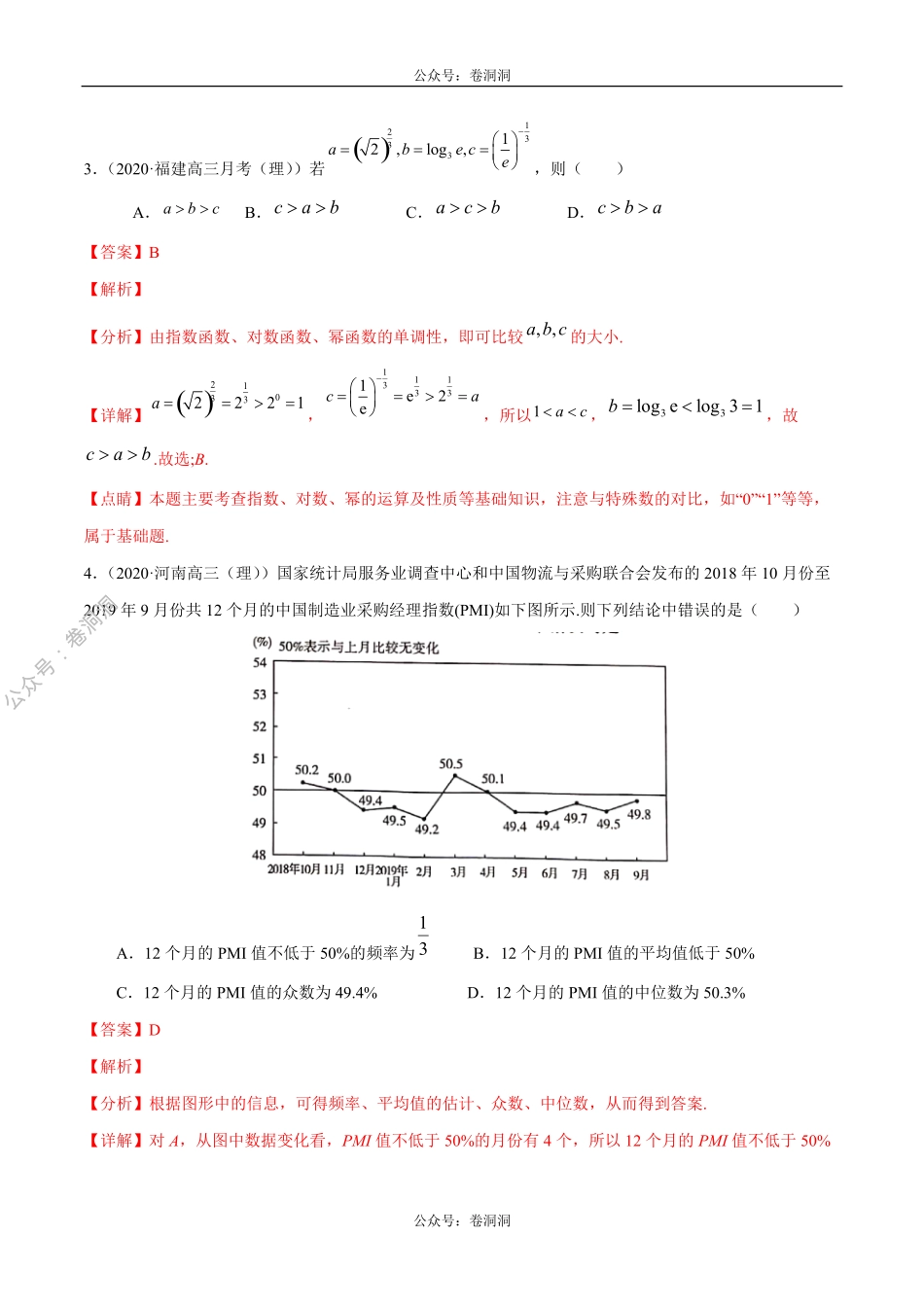
公众号：卷洞洞公众号：卷洞洞绝密★启用前|学科网考试研究中心命制2020年高三【名校、地市联考】精选仿真模拟卷07数学（理）（本试卷满分150分，考试用时120分钟）第I卷（选择题)一、单选题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。1．（2020·贵州高三月考（理））已知集合，，则（）23Axx2,1,0,1,2,3BABA．B．C．D．1,0,12,2,32,33【答案】B【解析】【分析】先化简集合，再求交集，即可得出结果.A【详解】因为或，，所以.233Axxxx3x2,1,0,1,2,3B2,2,3AB【点睛】本题主要考查集合交集的运算，熟记概念即可，属于基础题型.2．（2020·山西高三月考（理））已知复数z满足：（2＋i）z＝1－i，其中i是虚数单位，则z的共轭复数为（）A．－iB．＋i15351535C．D．13i13i【答案】B【解析】【分析】把等式变形，根据复数的运算先求出z，再根据共轭复数的定义得出答案.【详解】由（2＋i）z＝1－i，得z＝＝＝－i，∴＝＋i.选：B.12ii(1)(2)(2)(2)iiii1535z1535【点睛】本题考查复数的运算法则、共轭复数的定义.公众号：卷洞洞公众号：卷洞洞公众号：卷洞洞3．（2020·福建高三月考（理））若，则（）233131log,2,abeceA．B．C．D．abccabacbcba【答案】B【解析】【分析】由指数函数、对数函数、幂函数的单调性，即可比较的大小.,,abc【详解】，，所以，，故213032221a1311331e2eac1ac33logelog31b.故选;B.cab【点睛】本题主要考查指数、对数、幂的运算及性质等基础知识，注意与特殊数的对比，如“0”“1”等等，属于基础题.4．（2020·河南高三（理））国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是（）A．12个月的PMI值不低于50%的频率为B．12个月的PMI值的平均值低于50%13C．12个月的PMI值的众数为49.4%D．12个月的PMI值的中位数为50.3%【答案】D【解析】【分析】根据图形中的信息，可得频率、平均值的估计、众数、中位数，从而得到答案.【详解】对A，从图中数据变化看，PMI值不低于50%的月份有4个，所以12个月的PMI值不低于50%公众号：卷洞洞公众号：卷洞洞公众号：卷洞洞的频率为，故A正确...