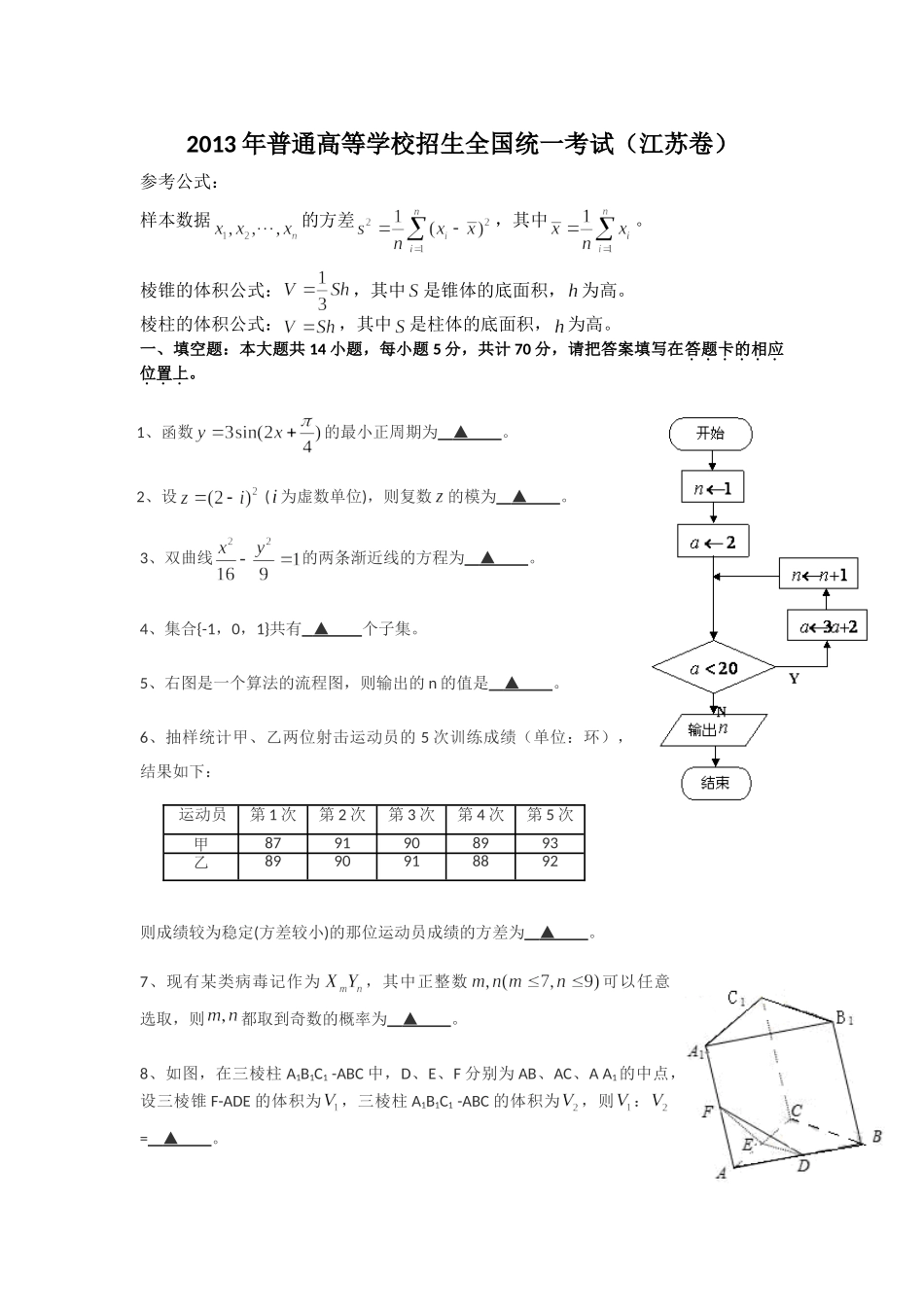
2013年普通高等学校招生全国统一考试(江苏卷)参考公式:样本数据的方差,其中。棱锥的体积公式:,其中是锥体的底面积,为高。棱柱的体积公式:,其中是柱体的底面积,为高。一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应位置上。1、函数的最小正周期为▲。2、设(为虚数单位),则复数的模为▲。3、双曲线的两条渐近线的方程为▲。4、集合{-1,0,1}共有▲个子集。5、右图是一个算法的流程图,则输出的n的值是▲。6、抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:则成绩较为稳定(方差较小)的那位运动员成绩的方差为▲。7、现有某类病毒记作为,其中正整数可以任意选取,则都取到奇数的概率为▲。8、如图,在三棱柱A1B1C1-ABC中,D、E、F分别为AB、AC、AA1的中点,设三棱锥F-ADE的体积为,三棱柱A1B1C1-ABC的体积为,则:=▲。运动员第1次第2次第3次第4次第5次甲8791908993乙89909188929、抛物线在处的切线与坐标轴围成三角形区域为D(包含三角形内部与边界)。若点P(x,y)是区域D内的任意一点,则的取值范围是▲。10、设D、E分别是△ABC的边AB、BC上的点,且。若(、均为实数),则+的值为▲。11、已知是定义在R上的奇函数。当时,,则不等式的解集用区间表示为▲。12、在平面直角坐标系xoy中,椭圆C的方程为,右焦点为F,右准线为,短轴的一个端点为B。设原点到直线BF的距离为,F到的距离为。若,则椭圆C的离心率为▲。13、在平面直角坐标系xoy中,设定点A(a,a),P是函数图象上的一动点。若点P、A之间的最短距离为,则满足条件的实数a的所有值为=▲。14、在正项等比数列中,,则满足的最大正整数n的值为▲。二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15、(本小题满分14分)已知向量。(1)若,求证:;(2)设,若,求的值。16、(本小题满分14分)如图,在三棱锥S-ABC中,平面平面SBC,,AS=AB。过A作,垂足为F,点E、G分别为线段SA、SC的中点。求证:(1)平面EFG//平面ABC;(2)。17、(本小题满分14分)如图,在平面直角坐标系xoy中,点A(0,3),直线,设圆C的半径为1,圆心在直线上。(1)若圆心C也在直线上,过点A作圆C的切线,求切线的方程;(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标的取值范围。18、(本小题满分16分)如图,游客从某旅游景区的景点A处下山至C处有两种路径。一种是从A沿直线步行到C,另一种是先...