2002年上海高考数学真题（文科）试卷（答案版）.doc

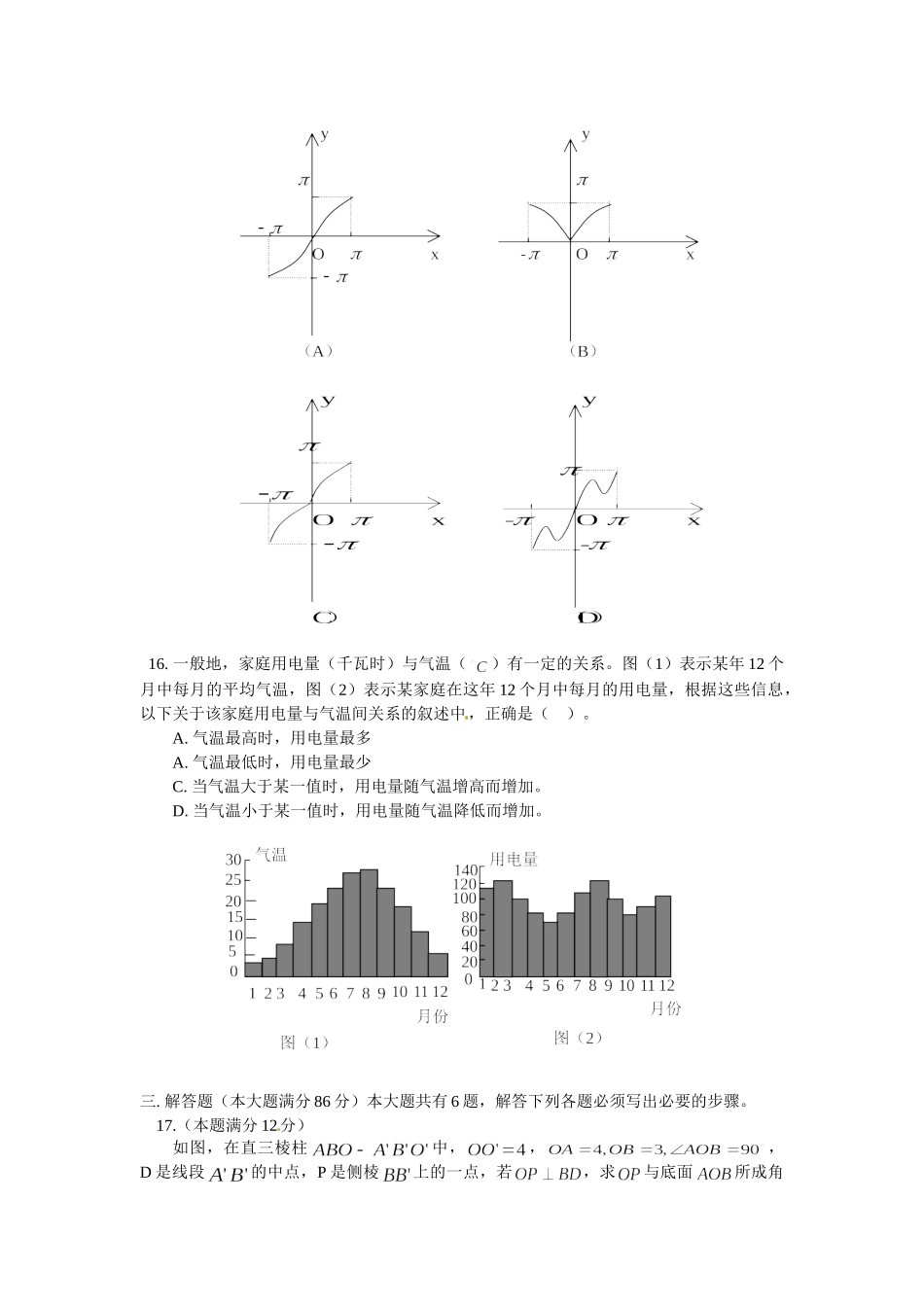
绝密★启用前 2002年普通高等学校招生全国统一考试（上海卷） 数学试卷(文史类) （满分150分，考试时间120分钟） 考生注意 1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页. 2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置. 3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分. 4.用2B铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题. 考生注意： 1. 答卷前，考生务必将姓名、高考准考证号、校验码等填写清楚。 2. 本试卷共有22道试题，满分150分，考试时间120分钟，请考生用钢笔或圆珠笔将答案直接写在试卷上。 一. 填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分。 1. 若（i为虚数单位），则 。 2. 已知向量的夹角为，且= 。 3. 方程的解x= 。 4. 若正四棱锥的底面边长为,体积为，则它的侧面与底面所成的二面角的大小是 。 5. 在二项式和的展开式中，各项系数之和分别记为、，n是正整数，则= 。 6. 已知圆和圆外一点，过点P作圆的切线，则两条切线夹角的正切值是 。 7. 在某次花样滑冰比赛中，发生裁判受贿事件，竞赛委员会决定将裁判由原来的9名增至14名，但只任取其中7名裁判的评分作为有效分，若14名裁判中有2人受贿，则有效分中没有受贿裁判的评分的概率是 （结果用数值表示） 8. 抛物线的焦点坐标是 。 9.某工程由下列工序组成，则工程总时数为 天。 工序 a b c d e f 紧前工序 — — a、b c c d、e 工时数（天） 2 3 2 5 4 1 10. 设函数，若是偶函数，则t的一个可能值是 。 11. 若数列中，（n是正整数），则数列的通项 。 12. 已知函数（定义域为D，值域为A）有反函数，则方程有解x=a，且的充要条件是满足 。 二. 选择题（本大题满分16分）本大题共有4题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分。 13. 如图，与复平面中的阴影部分（含边界）对应的复数集合是（ ） A. B. C. D. 14. 已知直线、m，平面、，且，给出下列四个命题。 （1）若 （2） （3）若，则 （3）若 其中正确命题的个数是（ ） A. 1个 B. 2个 C. 3个 D. 4个 15. 函数的大致图象是（ ） 16. 一般地，家庭用电量（千瓦时）与气温（）有一定的关系。图（1）表示某年12个月中每月的平均气温，图（2）表示某家庭在这年12个月中每月的用电量，根据这些信息，以下关于该家庭用电量与气温间关系的叙述中，正确是（ ）。 A. 气温最高时，用电量最多 A. 气温最低时，用电量最少 C. 当气温大于某一值时，用电量随气温增高而增加。 D. 当气温小于某一值时，用电量随气温降低而增加。 三. 解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤。 17.（本题满分12分） 如图，在直三棱柱中，，，D是线段的中点，P是侧棱上的一点，若，求与底面所成角的大小。（结果用反三角函数值表示） 18. （本题满分12分） 已知点，动点C到A、B两点的距离之差的绝对值为2，点C的轨迹与直线交于D、E两点，求线段DE的长。 19. （本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分。 已知函数 （1）当时，求函数的最大值与最小值。 （2）求实数a的取值范围，使在区间上是单调函数。 20. （本题满分14分）本题共有2个小题，第1小题满分4分，第2小题满分10分。 某商场在促销期间规定：商场内所有商品按标价的80%出售，同时，当顾客在该商场内消费满一定金额后，按如下方案获得相应金额的奖券： 消费金额（元）的范围 [200,400) [400,500) [500,700) [700,900) … 获得奖券的金额（元） 30 60 100 130 … 根据上述促销方法，顾客在该商场购物可以获得双重优惠，例如，购买标价为400元的商品，则消费金额为320元，获得的优惠额为：（元），设购买商品得到的优惠率。试问： （1）若购买一件标价为1000元的商品，顾客得到的优惠率是多少？ （2）对于标价在（元）内的商品，顾客购买标价为多少元的商品，可得到不小于的优惠率？ 21. （本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分。 已知函数的图象过点和。 （1）求函数f(x)的解析式。 （2）记，n是正整数，是数列的前n项和，解关于n的不等式； （3）对于（2）中的与，整数96是否为数列中的项？若是，则求出相应的项数；若不是，则说明理由。 22. （本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分。 规定，其中，m是正整数，且，这是组合数（n,m是正整数，且）的一种推广。 （1）求的值。 （2）设x>0，当x为何值时，取得最小值？ （3）组合数的两个性质： ① ；② 是否都能推广到（，m是正整数）的情形？若能推广，则写出推广的形式并给出证明；若不能，则说明理由。 答案要点 说明： 1. 本解答列出试题的一种或几种解法，如果考生的解法与所列解法不同，可参照解答中评分标准的精神进行评分。 2. 评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误，影响了后继部分，但该步以后的解答未改变这一题的内容和难度时，可视影响程度决定后面部分的给分，这时原则上不应超过后面部分应给分数之半，如果有较严重的概念性错误，就不给分。 一. （第1题至12题） 1. 2. 13 3. -1 4. 5. 6. 7. 8. （0，1） 9.11 10. 11. 12. ,且的图象在直线的下方，且与y轴的交点为。 二. （第13题至16题） 13. D 14. B 15. C 16. C 三. （第17题至第22题） 17. [解法一] 如图,以点为原点建立空间直角坐标系 由题意，有 设，则 因为 因为平面AOB 是OP与底面AOB所成的角 [解法二]取中点E，连结DE、BE，则 平面 是BD在平面内的射影。 又因为 由三垂线定理的逆定理，得 在矩形中，易得 得 （以下同解法一） 18. [解] 设点C（x,y），则 根据双曲线的定义，可知点C的轨迹是双曲线 由 故点C的轨迹方程是 由，得 因为，所以直线与双曲线有两个交点。 设、， 则 故 19. [解] （1）当时 时，的最小值为1 时，的最大值为37。 （2）函数图象的对称轴为 因为在区间上是单调函数。 故的取值范围是或 20. [解] （1） （2）设商品的标价为x元 则，消费额： 由已知得（I） 或（II） 不等式组（I）无解，不等式组（II）的解为 因此，当顾客购买标价在[625，750]元内的商品时，可得到不小于的优惠率。 21. [解] （1）由， 得 故 （2）由题意 l 由得，即 故 l （3），，， l 当时， l 当时， l 因此，96不是数列中的项。 l l 22. [解] （1） l （2） l l 因为 l 当且仅当时，等号成立。 l 当时，取得最小值。 l （3）性质（1）不能推广。 l 例如当时，有定义，但无意义； l 性质(2)能推广，它的推广形式是 l ，m是正整数，事实上 l 当m=1时，有 l 当时， l l [证明]（3）当时，组合数 当时， 当x<0时，