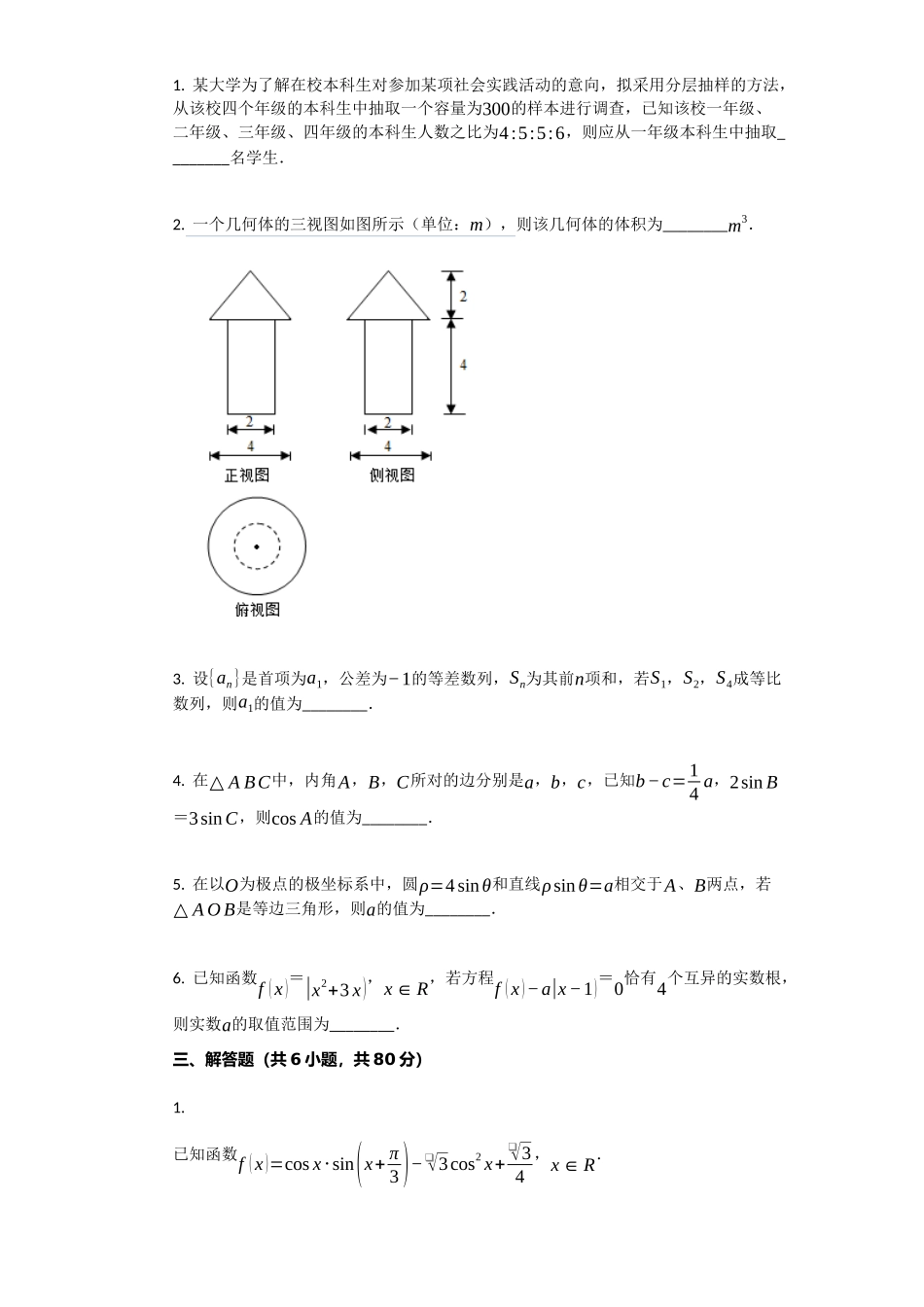
2014年天津市高考数学试卷(理科)一、选择题(共8小题,每小题5分)1.i是虚数单位,复数7+i3+4i=()A.1−iB.−1+iC.1725+3125iD.−177+257i2.设变量x,y满足约束条件{x+y−2≥0x−y−2≤0y≥1),则目标函数z=¿x+2y的最小值为()A.2B.3C.4D.53.阅读如图的程序框图,运行相应的程序,输出S的值为()A.15B.105C.245D.9454.函数f(x)=log12(x2−4)的单调递增区间为()A.(0,+∞)B.(−∞,0)C.(2,+∞)D.(−∞,−2)5.已知双曲线x2a2−y2b2=1(a>0,b>0)的一条渐近线平行于直线l:y=2x+10,双曲线的一个焦点在直线l上,则双曲线的方程为()A.x25−y220=1B.x220−y25=1C.3x225−3y2100=1D.3x2100−3y225=16.如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分∠CBF;②FB2=FD⋅FA;③AE⋅CE=BE⋅DE;④AF⋅BD=AB⋅BF.所有正确结论的序号是()A.①②B.③④C.①②③D.①②④7.设a,b∈R,则“a>b”是“a|a)>b|b)”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件8.已知菱形ABCD的边长为2,∠BAD=¿120∘,点E,F分别在边BC,DC上,BE→=λBC→,DF→=μDC→,若AE→⋅AF→=1,CE→⋅CF→=−23,则λ+μ=¿()A.12B.712C.23D.56二、填空题(共6小题,每小题5分,共30分)1.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查,已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取________名学生.2.一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.3.设{an}是首项为a1,公差为−1的等差数列,Sn为其前n项和,若S1,S2,S4成等比数列,则a1的值为________.4.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知b−c=14a,2sinB=3sinC,则cosA的值为________.5.在以O为极点的极坐标系中,圆ρ=4sinθ和直线ρsinθ=a相交于A、B两点,若△AOB是等边三角形,则a的值为________.6.已知函数f(x)=|x2+3x),x∈R,若方程f(x)−a|x−1)=0恰有4个互异的实数根,则实数a的取值范围为________.三、解答题(共6小题,共80分)1.已知函数f(x)=cosx⋅sin(x+π3)−❑√3cos2x+❑√34,x∈R.(1)求f(x)的最小正周期;(2)求f(x)在闭区间[−π4,π4]上的最大值和最小值.2.某大学志愿者协会有6名男同...