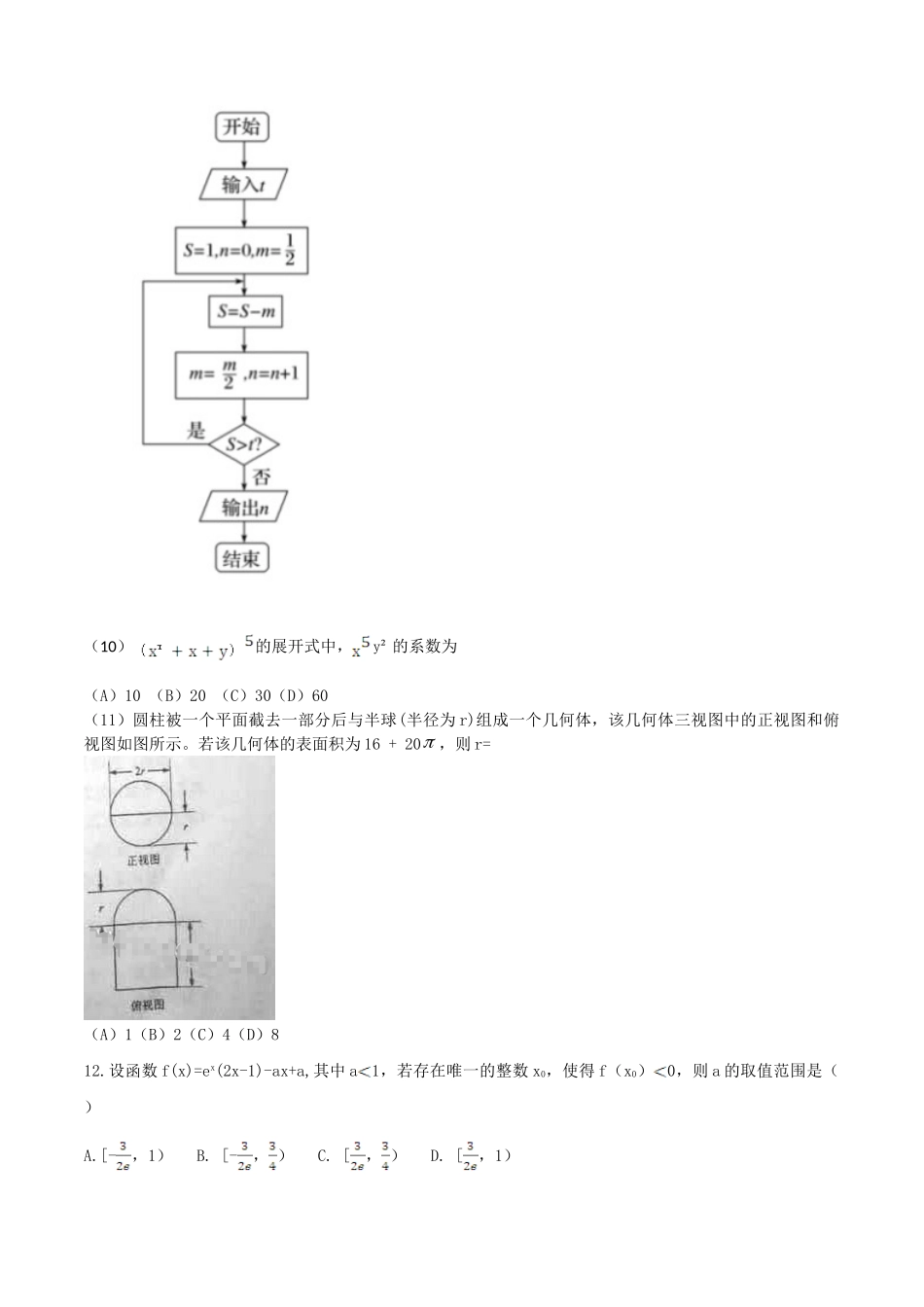
2015年江西高考理科数学试题及答案注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至3页,第Ⅱ卷3至5页。2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。3.全部答案在答题卡上完成,答在本试题上无效。4.考试结束后,将本试题和答题卡一并交回。第Ⅰ卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。(1)设复数z满足1+z1z=i,则|z|=(A)1(B)2(C)3(D)2(2)sin20°cos10°-cos160°sin10°=(A)32(B)32(C)12(D)12(3)设命题P:nN,2n>2n,则P为(A)nN,2n>2n(B)nN,2n≤2n(C)nN,2n≤2n(D)nN,2n=2n(4)投篮测试中,每人投3次,至少投中2次才能通过测试。已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为(A)0.648(B)0.432(C)0.36(D)0.312(5)已知M(x0,y0)是双曲线C:2212xy上的一点,F1、F2是C上的两个焦点,若1MF�2MF�<0,则y0的取值范围是(A)(-33,33)(B)(-36,36)(C)(223,223)(D)(233,233)(6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有A.14斛B.22斛C.36斛D.66斛(7)设D为ABC所在平面内一点=3,则(A)=+(B)=(C)=+(D)=(8)函数f(x)=的部分图像如图所示,则f(x)的单调递减区间为(A)(),k(b)(),k(C)(),k(D)(),k(9)执行右面的程序框图,如果输入的t=0.01,则输出的n=(A)5(B)6(C)7(D)8(10)的展开式中,y²的系数为(A)10(B)20(C)30(D)60(11)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示。若该几何体的表面积为16+20,则r=(A)1(B)2(C)4(D)812.设函数f(x)=ex(2x-1)-ax+a,其中a1,若存在唯一的整数x0,使得f(x0)0,则a的取值范围是()A.[-,1)B.[-,)C.[,)D.[,1)第II卷本卷包括必考题和选考题两部分。第(13)题~第(21)题为必考题,每个试题考生都必须作答。第(22)题~第(2...