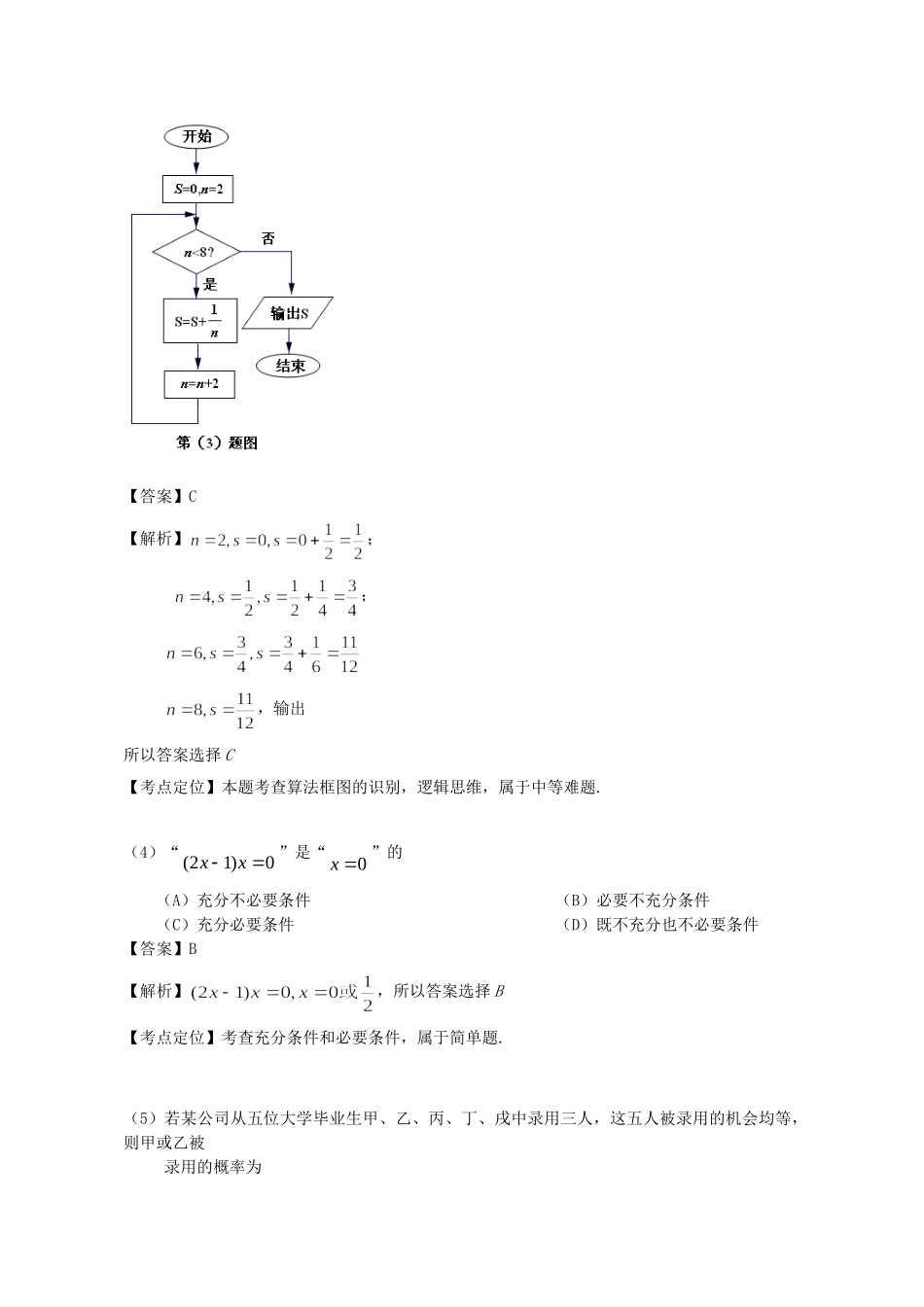
2013年安徽高考文科数学试题及答案[详细解析]一.选择题选择题:本大题共10小题。每小题5分,共50分。在每个小题给出的四个选项中,只有一项是符合题目要求的。(1)设i是虚数单位,若复数10()3aaRi是纯虚数,则a的值为()(A)-3(B)-1(C)1(D)3【答案】D【解析】,所以a=3,故选择D【考点定位】考查纯虚数的概念,及复数的运算,属于简单题.(2)已知|10,2,1,0,1AxxB,则()RCAB()(A)2,1(B)2(C)1,0,1(D)0,1【答案】A【解析】A:,,,所以答案选A【考点定位】考查集合的交集和补集,属于简单题.(3)如图所示,程序据图(算法流程图)的输出结果为(A)34(B)16(C)1112(D)2524【答案】C【解析】;;,输出所以答案选择C【考点定位】本题考查算法框图的识别,逻辑思维,属于中等难题.(4)“(21)0xx”是“0x”的(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件【答案】B【解析】,所以答案选择B【考点定位】考查充分条件和必要条件,属于简单题.(5)若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为(A)23(B)25(C)35(D)910【答案】D【解析】总的可能性有10种,甲被录用乙没被录用的可能性3种,乙被录用甲没被录用的可能性3种,甲乙都被录用的可能性3种,所以最后的概率333110p【考点定位】考查古典概型的概念,以及对一些常见问题的分析,简单题.(6)直线2550xy被圆22240xyxy截得的弦长为(A)1(B)2(C)4(D)46【答案】C【解析】圆心(1,2),圆心到直线的距离1+4-5+5=15d,半径5r,所以最后弦长为222(5)14.【考点定位】考查解析几何初步知识,直线与圆的位置关系,点到直线的距离,简单题.(7)设nS为等差数列na的前n项和,8374,2Saa,则9a=(A)6(B)4(C)2(D)2【答案】A【解析】188333636978()4420226aaSaaaaaadaad【考点定位】考查等差数列通项公式和前n项公式的应用,以及数列基本量的求解.(8)函数()yfx的图像如图所示,在区间,ab上可找到(2)nn个不同的数12,,,nxxx,使得1212()()()nnfxfxfxxxx,则n的取值范围为(A)2,3(B)2,3,4(C)3,4(D)3,4,5【答案】B【解析】1111()()00fxfxxx表示11(,())xfx到原点的斜率;1212()()()nnfx...