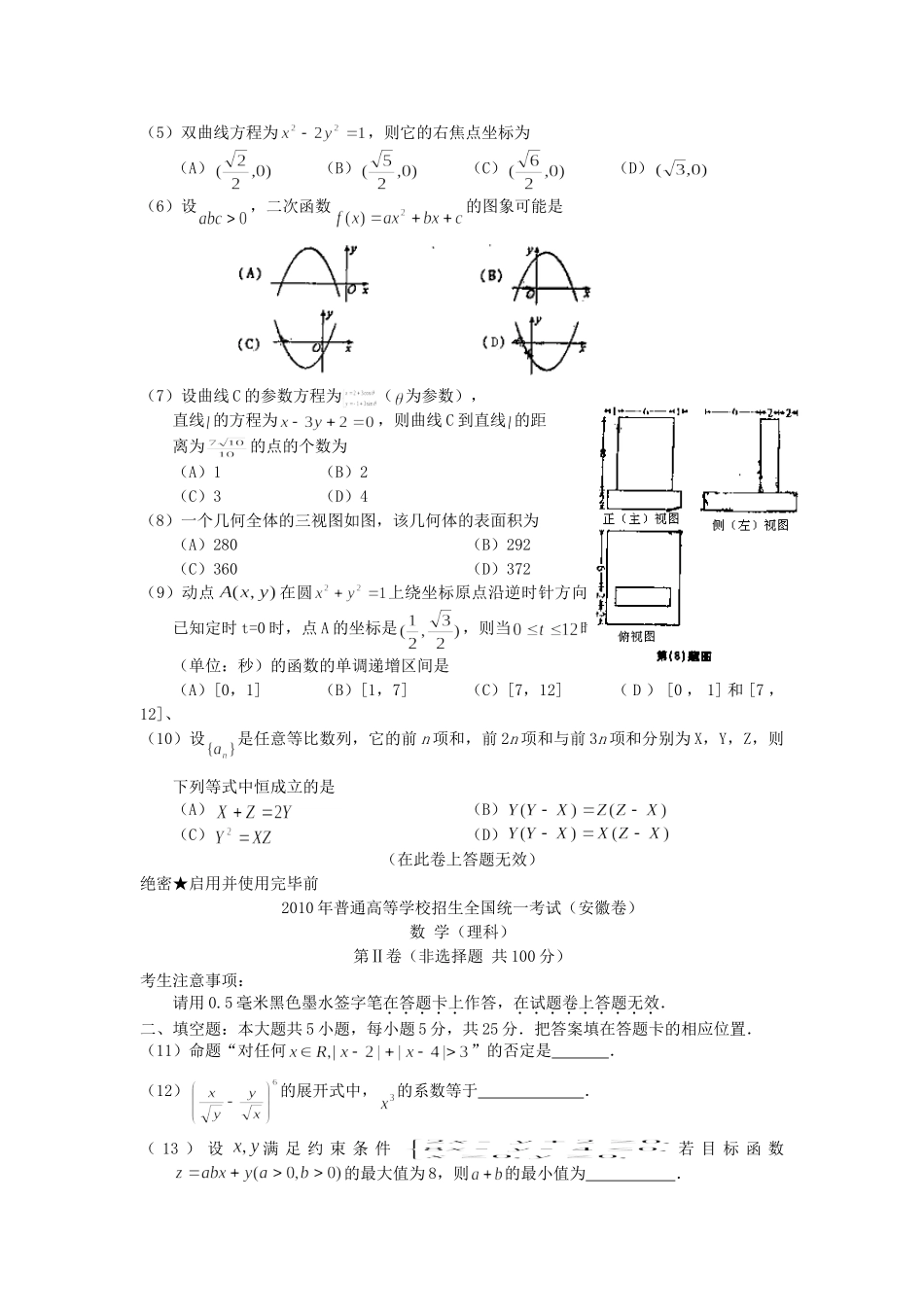
2010年安徽高考理科数学真题及答案本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分.考试用时120分钟.注意事项:1.答卷前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致.务必在答题卡背面规定的地方填写姓名和座位号后两位.2.答第I卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3.答第Ⅱ卷时,必须使用0.5毫米黑色黑水签字笔在答题卡上书写,要求字体工整、笔迹清晰.作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色签际笔描清楚.必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效.4.考试结束,务必将试题卷和答题卡一并上交.参考公式:如果事件A与B互斥,那么如果A与B是两个任意事件,,那么如果事件A与B相互独立,那么第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)是虚数单位,(A)(B)(C)(D)(2)若集合,则(A)(B)(C)(D)(3)设向量,则下列结论中正确的是(A)(B)(C)垂直(D)(4)若是R上周期为5的奇函数,且满足则=(A)-1(B)1(C)-2(D)2(5)双曲线方程为,则它的右焦点坐标为(A)(B)(C)(D)(6)设,二次函数的图象可能是(7)设曲线C的参数方程为(为参数),直线的方程为,则曲线C到直线的距离为的点的个数为(A)1(B)2(C)3(D)4(8)一个几何全体的三视图如图,该几何体的表面积为(A)280(B)292(C)360(D)372(9)动点在圆上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知定时t=0时,点A的坐标是,则当时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是(A)[0,1](B)[1,7](C)[7,12](D)[0,1]和[7,12]、(10)设是任意等比数列,它的前n项和,前2n项和与前3n项和分别为X,Y,Z,则下列等式中恒成立的是(A)(B)(C)(D)(在此卷上答题无效)绝密★启用并使用完毕前2010年普通高等学校招生全国统一考试(安徽卷)数学(理科)第Ⅱ卷(非选择题共100分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置.(11)命题...