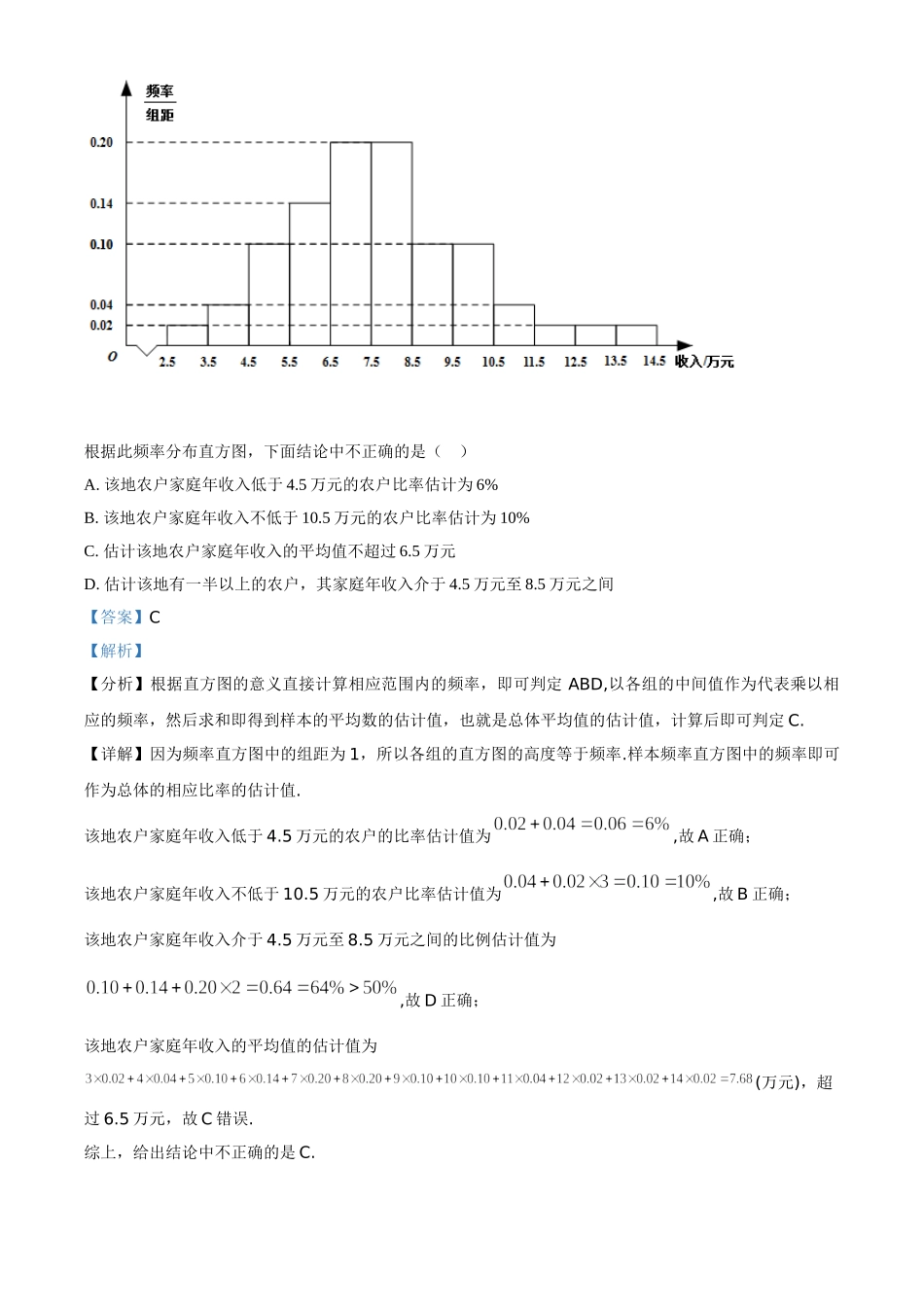
绝密★启用前2021年普通高等学校招生全国统一考试(甲卷)文科数学注意事项:1.答卷前,考生务必将自己的姓名准考证号填写在答题卡上、.2.回答选择题时,选出每小题答案后,用铅笔把题卡上对应题目的答案标号涂黑.如需改动,用皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一选择题:本题共、12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,则()A.B.C.D.【答案】B【解析】【分析】求出集合后可求.【详解】,故,故选:B.2.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是()A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间【答案】C【解析】【分析】根据直方图的意义直接计算相应范围内的频率,即可判定ABD,以各组的中间值作为代表乘以相应的频率,然后求和即得到样本的平均数的估计值,也就是总体平均值的估计值,计算后即可判定C.【详解】因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.该地农户家庭年收入低于4.5万元的农户的比率估计值为,故A正确;该地农户家庭年收入不低于10.5万元的农户比率估计值为,故B正确;该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为,故D正确;该地农户家庭年收入的平均值的估计值为(万元),超过6.5万元,故C错误.综上,给出结论中不正确的是C.故选:C.【点睛】本题考查利用样本频率直方图估计总体频率和平均值,属基础题,样本的频率可作为总体的频率的估计值,样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值,可以作为总体的平均值的估计值.注意各组的频率等于.3.已知,则()A.B.C.D.【答案】B【解析】【分析】由已知得,根据复数除法运算法则,即可求解.【详解】,.故选:B.4.下列函数中是增函数的为()A.B.C.D.【答案】D【解析】【分析】根据基本初等函数的性质逐项判断后可得正确的选项.【详解】对于A,为上的减函数,不合题意,舍.对于B,为上的减函数,不合题意,舍.对于C...