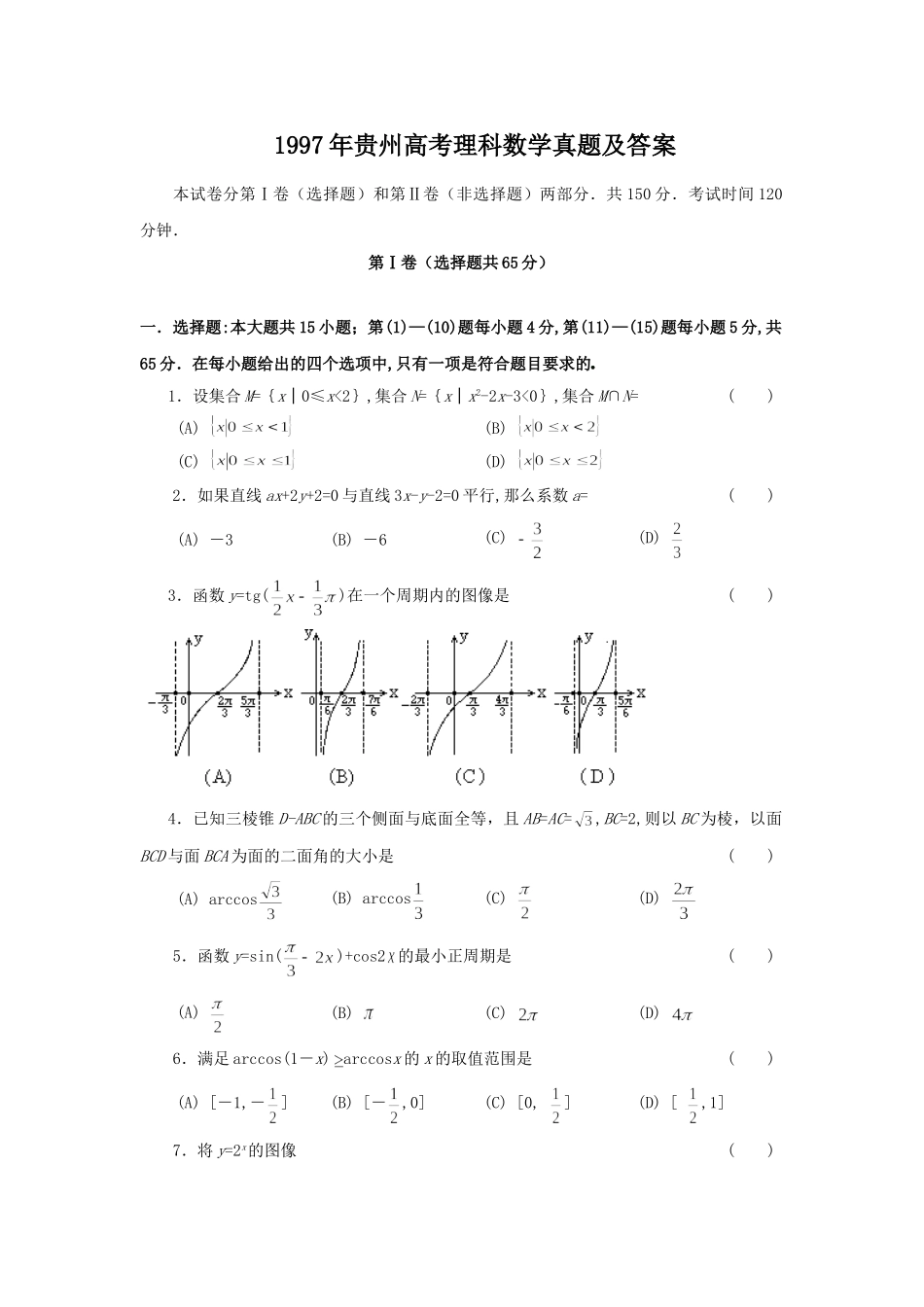
1997年贵州高考理科数学真题及答案.doc

1997年贵州高考理科数学真题及答案 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分．考试时间120分钟． 第Ⅰ卷（选择题共65分） 一．选择题:本大题共15小题；第(1)—(10)题每小题4分,第(11)—(15)题每小题5分,共65分．在每小题给出的四个选项中,只有一项是符合题目要求的 1．设集合M=｛x│0≤x<2｝,集合N=｛x│x2-2x-3<0｝,集合M∩N= ( ) (A) (B) (C) (D) 2．如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a= ( ) (A) －3 (B) －6 (C) (D) 3．函数y=tg()在一个周期内的图像是 ( ) 4．已知三棱锥D-ABC的三个侧面与底面全等，且AB=AC=,BC=2,则以BC为棱，以面BCD与面BCA为面的二面角的大小是 ( ) (A) arccos (B) arccos (C) (D) 5．函数y=sin()+cos2的最小正周期是 ( ) (A) (B) (C) (D) 6．满足arccos(1－x)arccosx的x的取值范围是 ( ) (A) [－1,－] (B) [－,0] (C) [0, ] (D) [ ,1] 7．将y=2x的图像 ( ) (A) 先向左平行移动1个单位 (B) 先向右平行移动1个单位 (C) 先向上平行移动1个单位 (D) 先向下平行移动1个单位 再作关于直线y=x对称的图像，可得到函数y=log2(x+1)的图像． 8．长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上，这个球的表面积是 ( ) (A) 20 (B) 25 (C) 50 (D) 200 9．曲线的参数方程是 (t是参数，t0),它的普通方程是 ( ) (A) (x－1)2(y－1)=1 (B) y= (C) (D) 10．函数y=cos2x-3cosx+2的最小值为 ( ) (A) 2 (B) 0 (C) (D) 6 11．椭圆C与椭圆关于直线x+y=0对称,椭圆C的方程是 ( ) (A) (B) (C) (D) 12．圆台上、下底面积分别为、,侧面积为,这个圆台的体积是 ( ) (A) (B) (C) (D) 13．定义在区间的奇函数f(x)为增函数；偶函数g(x)在区间[）的图像与f(x)的图像重合，设a>b>0,给出下列不等式： ①f(b)－f(－a)>g(a)－g(－b)； ②f(b)－f(－a)<g(a)－g(－b)； ③f(a)－f(－b)>g(b)－g(－a)； ④f(a)－f(－b)<g(b)－g(－a)， 其中成立的是 ( ) (A) ①与④ (B) ②与③ (C) ①与③ (D) ②与④ 14．不等式组 的解集是 ( ) (A) (B) (C) (D) 15．四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，不同的取法共有 ( ) (A) 150种 (B) 147种 (C) 144种 (D) 141种 第Ⅱ卷 (非选择题共85分) 二．填空题:本大题共4小题;每小题4分,共16分．把答案填在题中横线上． 16．已知的展开式中的系数为,常数a的值为________ 17．已知直线的极坐标方程为sin()=,则极点到该直线的距离是_____ 18．的值为_______ 19．已知m,l是直线，、是平面，给出下列命题： ①若l垂直于内的两条相交直线，则l； ②若l平行于,则l平行于内的所有直线； ③若,,且,则； ④若,且,则； ⑤若,,且∥,则∥． 其中正确的命题的序号是_______ (注:把你认为正确的命题的序号都填上) 三．解答题:本大题共6小题;共69分．解答应写出文字说明、证明过程或演算步骤． 20．(本小题满分10分) 已知复数,．复数,在复数平面上所对应的点分别为P,Q．证明是等腰直角三角形（其中为原点）． 21．(本小题满分11分) 已知数列,都是由正数组成的等比数列，公比分别为p、q,其中p> q,且，．设,Sn为数列的前n项和．求． 22．（本小题满分12分） 甲、乙两地相距S千米，汽车从甲地匀速行驶到乙地，速度不得超过c千米/时．已 知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度v (千米/时)的平方成正比、比例系数为b；固定部分为a元． I．把全程运输成本y（元）表示为速度v（千米/时）的函数，并指出这个函数的定 义域； II．为了使全程运输成本最小，汽车应以多大速度行驶？ 23．（本小题满分12分） 如图，在正方体ABCD-A1B1C1D1中，E、F分别是BB1、CD的中点． I．证明ADD1F； II．求AE与D1F所成的角； III．证明面AED面A1FD1； IV．设AA1=2,求三棱锥F-A1ED1的体积 24．(本小题满分12分) 设二次函数f(x)=ax2+bx+c(a>0),方程f(x)－x=0的两个根x1,x2满足0<x1<x2<． I．当x(0, x1)时，证明x<f (x)<x1； II．设函数f(x)的图像关于直线x=x0对称，证明x0<25． (25)（本小题满分12分） 设圆满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3:1，在满足条件①、②的所有圆中，求圆心到直线l:x-2y=0的距离最小的圆的方程． 1997年普通高等学校招生全国统一考试 数学试题(理工农医类)参考解答及评分标准 一．选择题:本题考查基本知识和基本运算． 1．B 2．B 3．A 4．C 5．B 6．D 7．D 8．C 9．B 10．B 11．A 12．D 13．C 14．C 15．D 二．填空题:本题考查基本知识和基本运算． 16．4 17． 18． 19．①，④ 注:第(19)题多填、漏填和错填均给0分． 三．解答题 20．本小题主要考查复数的基本概念、复数的运算以及复数的几何意义等基础知识，考查运算能力和逻辑推理能力． 解法一： 于是 因为OP与OQ的夹角为，所以OP⊥OQ． 因为，所以 由此知△OPQ有两边相等且其夹角为直角，故△OPQ为等腰直角三角形． 解法二: 因为，所以． 因为，所以 于是 由此得OP⊥OQ，│OP│=│OQ│． 由此知△OPQ有两边相等且其夹角为直角，故△OPQ为等腰直角三角形． (21)本小题主要考查等比数列的概念、数列极限的运算等基础知识，考查逻辑推理能力和运算能力．满分11分． 解: ． 分两种情况讨论． (Ⅰ)p>1． ∵ = =p． (Ⅱ)p<1． ∵ 0<q<p<1， (22)本小题主要考查建立函数关系、不等式性质、最大值、最小值等基础知识，考查综合应用所学数学知识、思想和方法解决实际问题的能力，满分12分． 解：（Ⅰ）依题意知汽车从甲地匀速行驶到乙地所用时间为，全程运输成本为 故所求函数及其定义域为 (Ⅱ)依题意知S，a，b，v都为正数，故有 当且仅当．即时上式中等号成立 若，则当时，全程运输成本y最小， 若，则当时，有 = 因为c－v≥0，且a>bc2，故有a－bcv≥a－bc2>0， 所以，且仅当v=c时等号成立， 也即当v=c时，全程运输成本y最小． 综上知，为使全程运输成本y最小，当时行驶速度应为；当时行驶速度应为v=c． (23)本小题主要考查直线与直线、直线与平面、平面与平面的位置关系，考查逻辑推理能力和空间想象能力，满分12分． 解:(Ⅰ)∵AC1是正方体， ∴AD⊥面DC1． 又D1F面DC1， ∴AD⊥D1F． (Ⅱ)取AB中点G，连结A1G，FG．因为F是CD的中点，所以GF、AD平行且相等，又A1D1、AD平行且相等，所以GF、A1D1平行且相等，故GFD1A1是平行四边形，A1G∥D1F． 设A1G与AE相交于点H，则∠AHA1是AE与D1F所成的角，因为E是BB1的中点，所以Rt△A1AG≌Rt△ABE，∠GA1A=∠GAH，从而∠AHA1=90°，即直线AE与D1F所成角为直角． (Ⅲ)由(Ⅰ)知AD⊥D1F，由(Ⅱ)知AE⊥D1F，又AD∩AE=A，所以D1F⊥面AED．又因为D1F面A1FD1，所以面AED⊥面A1FD1． (Ⅳ)连结GE，GD1． ∵FG∥A1D1，∴FG∥面A1ED1， ∴ ∵AA1=2， ∴正方形ABB1A1 (24)本小题主要考查一元二次方程、二次函数和不等式的基础知识，考查综合运用数学知识分析问题和解决问题的能力．满分12分． 证明:(Ⅰ)令F(x)=f(x)－x．因为x1，x2是方程f(x)－x=0的根，所以 F(x)=a(x－x1)(x－x2)． 当x∈(0，x1)时，由于x1<x2，得(x－x1)(x－x2)>0，又a>0，得 F(x)=a(x－x1)(x－x2)>0， 即x<f(x)． 因为 所以x1－x>0，1+a(x－x2)=1+ax－ax2>1－ax2>0． 得 x1－f(x)>0． 由此得f(x)<x1． (Ⅱ)依题意知 因为x1，x2是方程f(x)－x=0的根，即x1，x2是方程ax2+(b－1)x+c=0的根． ∴， 因为ax2<1，所以． (25)本小题主要考查轨迹的思想，求最小值的方法，考查综合运用知识建立曲线方程的能力．满分12分． 解法一:设圆的圆心为P(a，b)，半径为r，则点P到x轴，y轴的距离分别为│b│， │a│． 由题设知圆P截x轴所得劣弧对的圆心角为90°，知圆P截X轴所得的弦长为，故r2=2b2， 又圆P截y轴所得的弦长为2，所以有 r2=a2+1． 从而得2b2－a2=1． 又点P(a，b)到直线x－2y=0的距离为 ， 所以5d2=│a－2b│2 =a2+4b2－4ab ≥a2+4b2－2(a2+b2) =2b2－a2=1， 当且仅当a=b时上式等号成立，此时5d2=1，从而d取得最小值． 由此有 解此方程组得 或 由于r2=2b2知． 于是，所求圆的方程是 (x－1) 2+(y－1) 2=2，或(x+1) 2+(y+1) 2=2． 解法二:同解法一，得 ∴ 得 ① 将a2=2b2－1代入①式，整理得 ② 把它看作b的二次方程，由于方程有实根，故判别式非负，即 △=8(5d2－1)≥0， 得 5d2≥1． ∴5d2有最小值1，从而d有最小值． 将其代入②式得2b2±4b+2=0．解得b=±1． 将b=±1代入r2=2b2，得r2=2．由r2=a2+1得a=±1． 综上a=±1，b=±1，r2=2． 由=1知a，b同号． 于是，所求圆的方程是 (x－1) 2+(y－1) 2=2，或(x+1) 2+(y+1) 2=2．