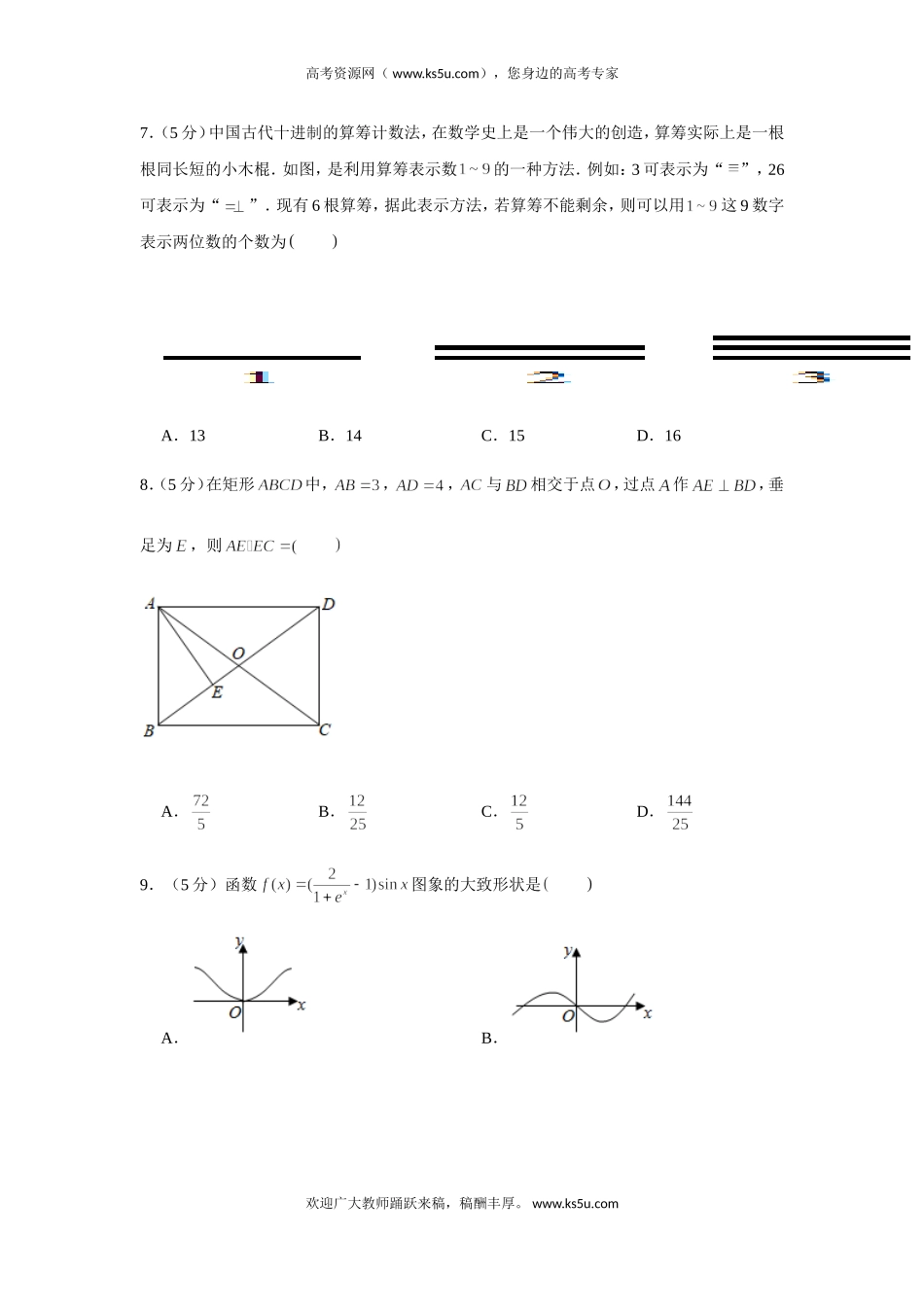
高考资源网(www.ks5u.com),您身边的高考专家2020年广东省广州市天河区高考数学一模试卷(理科)一、选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合,集合,则A.,B.,C.D.2.(5分)设复数满足,则复数在复平面内对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)设等差数列的前项和为,若,则等于A.18B.36C.45D.604.(5分)已知,是两条不同的直线,,,是三个不同的平面,则下列命题正确的是A.若,,则B.若,,则C.若,,且,,则D.若,,且,则5.(5分)的展开式的常数项是A.B.C.2D.36.(5分)已知,,满足,则下列各选项正确的是A.B.C.D.欢迎广大教师踊跃来稿,稿酬丰厚。www.ks5u.com高考资源网(www.ks5u.com),您身边的高考专家7.(5分)中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数的一种方法.例如:3可表示为“”,26可表示为“”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用这9数字表示两位数的个数为A.13B.14C.15D.168.(5分)在矩形中,,,与相交于点,过点作,垂足为,则A.B.C.D.9.(5分)函数图象的大致形状是A.B.欢迎广大教师踊跃来稿,稿酬丰厚。www.ks5u.com高考资源网(www.ks5u.com),您身边的高考专家C.D.10.(5分)2位男生和3位女生共5位同学站成一排,若3位女生中有且只有两位女生相邻,则不同排法的种数是A.36B.24C.72D.14411.(5分)已知函数,若方程的解为,,则A.B.C.D.12.(5分)已知函数,,,曲线上总存在两点,,,,使曲线在,两点处的切线互相平行,则的取值范围为A.B.C.D.二、填空题:本大题共4小题,每小题5分,满分20分.13.(5分)已知数列满足,,则当时,.14.(5分)设当时,函数取得最大值,则.15.(5分)已知函数在处有极小值10,则.欢迎广大教师踊跃来稿,稿酬丰厚。www.ks5u.com高考资源网(www.ks5u.com),您身边的高考专家16.(5分)在三棱锥中,,侧面与底面垂直,则三棱锥外接球的表面积是.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题学生都必须作答。第22、23题为选考题,考生根据要求作答。(一)必考题:共60分。17.(12分)在锐角中,角,,对应的边分别是,,,且.(1)求角的大小;...