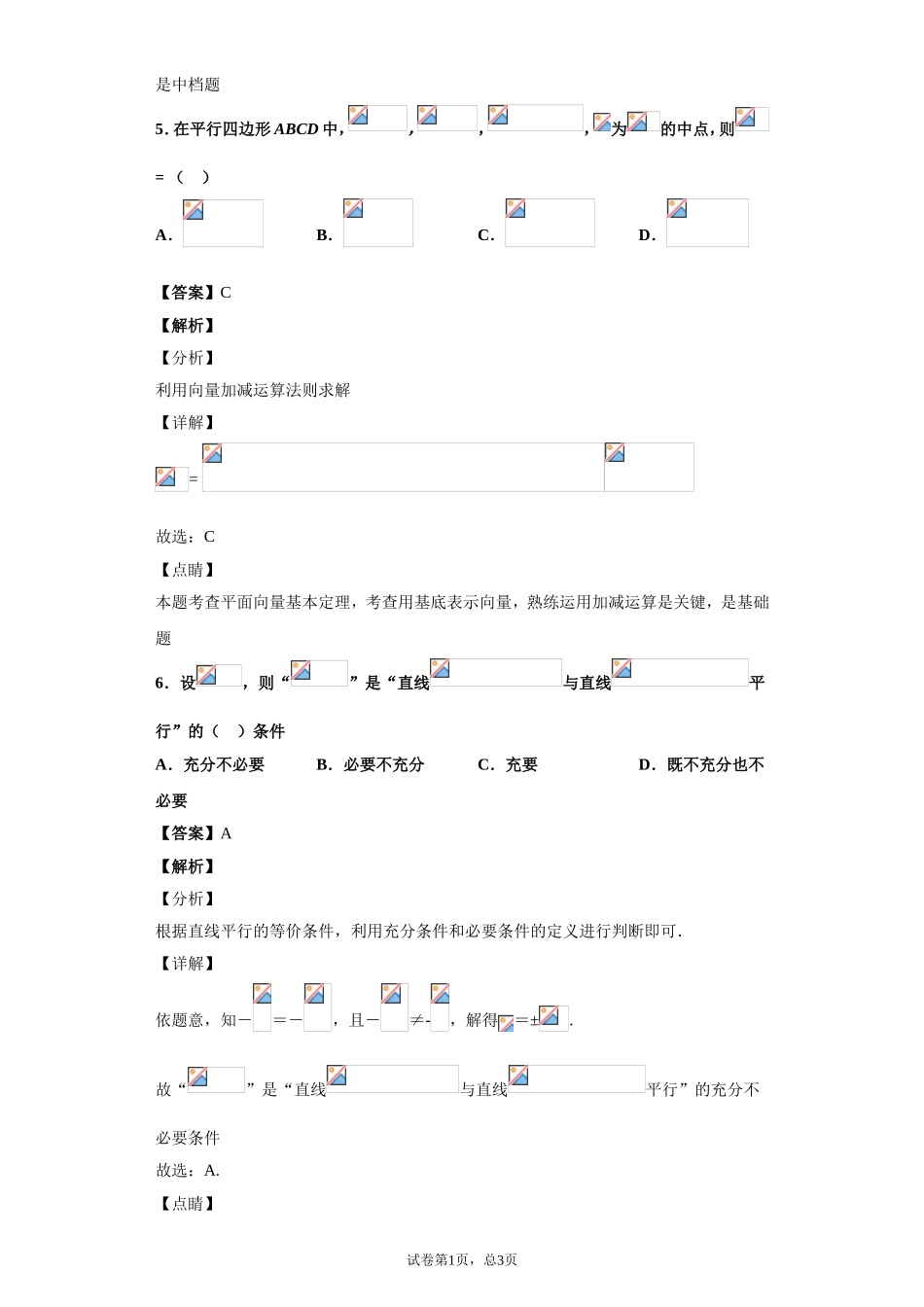
2020年1月2日高中数学作业一、单选题1.已知全集,,则()A.B.C.D.【答案】D【解析】【分析】化简集合,再求补集即可【详解】,,故选:D.【点睛】本题考查补集运算,考查指数不等式解法,是基础题2.设i为虚数单位,复数,则在复平面内对应的点在第()象限A.一B.二C.三D.四【答案】B【解析】【分析】先根据复数乘法求复数代数形式,再确定象限.【详解】,所以在复平面内对应的点为,在第二象限.故选:B【点睛】本题考查复数乘法运算以及复数几何意义,考查基本分析求解能力,属基础题.试卷第1页,总3页3.已知,,,则()A.B.C.D.【答案】D【解析】【分析】利用指数与对数的性质与0,1比较即可【详解】,,,所以.故选:D.【点睛】本题考查指数与对数的单调性,插入中间值与0,1比较是常用方法,是基础题4.在直角坐标系中,已知角θ的顶点与原点重合,始边与x轴的非负半轴重合,终边落在直线上,则=()A.B.C.D.【答案】A【解析】【分析】由终边确定角的正切值,利用诱导公式及二倍角公式求解【详解】因为角θ终边落在直线上,所以,,所以故选:A.【点睛】本题考查三角函数的定义,考查二倍角公式及诱导公式,意在考查计算能力及公式运用,试卷第1页,总3页是中档题5.在平行四边形ABCD中,,,,为的中点,则=()A.B.C.D.【答案】C【解析】【分析】利用向量加减运算法则求解【详解】=故选:C【点睛】本题考查平面向量基本定理,考查用基底表示向量,熟练运用加减运算是关键,是基础题6.设,则“”是“直线与直线平行”的()条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要【答案】A【解析】【分析】根据直线平行的等价条件,利用充分条件和必要条件的定义进行判断即可.【详解】依题意,知-=-,且-≠-,解得=±.故“”是“直线与直线平行”的充分不必要条件故选:A.【点睛】试卷第1页,总3页本题主要考查充分条件和必要条件的判断,利用直线平行的等价关系是解决本题的关键.7.数列:1,1,2,3,5,8,13,21,34,…,称为斐波那契数列,是由十三世纪意大利数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”.该数列从第三项开始,每项等于其前相邻两项之和.即:.记该数列的前项和为,则下列结论正确的是()A.B.C.D.【答案】D【解析】【分析】根据递推关系利用裂项相消法探求和项与通项关系,即得结果.【详解】因为,所以,选D.【点睛】本题考查裂项相消法,考查基本分...