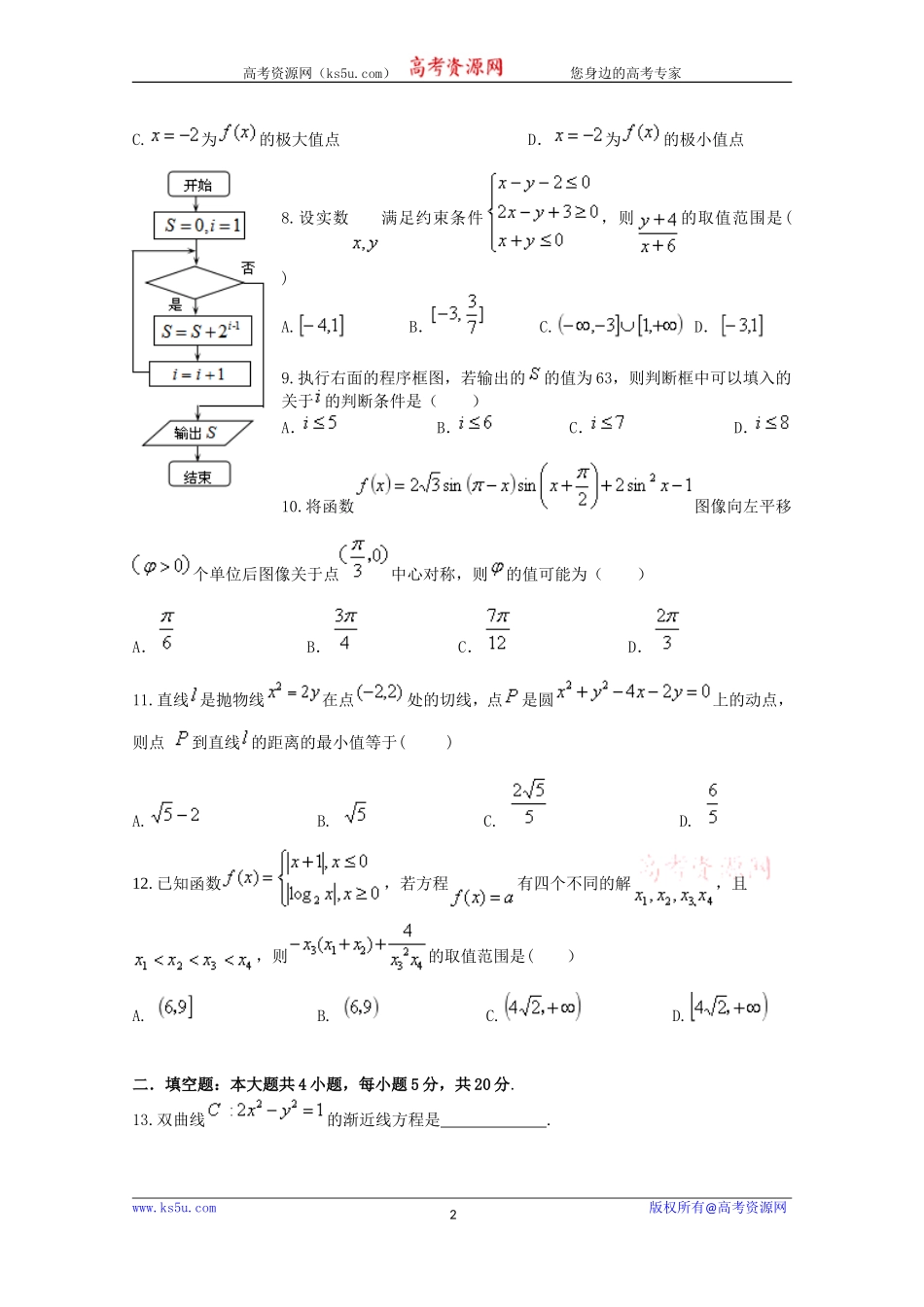
高考资源网(ks5u.com)您身边的高考专家数学试题文注意事项:1.答卷前,考生务必将自己的姓名考号填写在答题卡上;2.作答时,务必将答案写在答题卡上,写在本试卷及草稿纸上无效;3.考试结束后,将答题卡交回。一.选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项是符合题目要求的.1.已知集合,,则=()A.B.C.D.2.已知复数满足(是虚数单位),则=()A.B.C.D.3.“为真命题”是“为真命题”()的条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要4.若,,,则实数的大小关系为()A.B.C.D.5.已知直线,直线为,若则()A.或B.C.D.或6.轴截面为正方形的圆柱的外接球的体积与该圆柱的体积的比值为()A.B.C.D.7.设函数,则()A.为的极大值点B.为的极小值点www.ks5u.com版权所有@高考资源网1高考资源网(ks5u.com)您身边的高考专家C.为的极大值点D.为的极小值点8.设实数满足约束条件,则的取值范围是()A.B.C.D.9.执行右面的程序框图,若输出的的值为63,则判断框中可以填入的关于的判断条件是()A.B.C.D.10.将函数图像向左平移个单位后图像关于点中心对称,则的值可能为()A.B.C.D.11.直线是抛物线在点处的切线,点是圆上的动点,则点到直线的距离的最小值等于()A.B.C.D.12.已知函数,若方程有四个不同的解,且,则的取值范围是()A.B.C.D.二.填空题:本大题共4小题,每小题5分,共20分.13.双曲线的渐近线方程是.www.ks5u.com版权所有@高考资源网2高考资源网(ks5u.com)您身边的高考专家14.平面向量的夹角为,且,则____15.已知是等差数列,,且.若,则的前项和.16.给出下列4个命题:①若函数在在上有零点,则一定有;②函数既不是奇函数又不是偶函数;③若函数的值域为,则实数的取值范围是;④若函数满足条件则的最小值为.其中正确命题的序号是:.(写出所有正确命题的序号)三.解答题:本大题共6小题,共70分.17.(本小题满分12分)中,内角对应的边分别为,满足.(Ⅰ)已知求与的值;(Ⅱ)若且求.18.(本小题满分12分)改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).www.ks5u.com版权所有@高考资源网3高考资源网(ks5u.com)您身边的高考专家(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值...