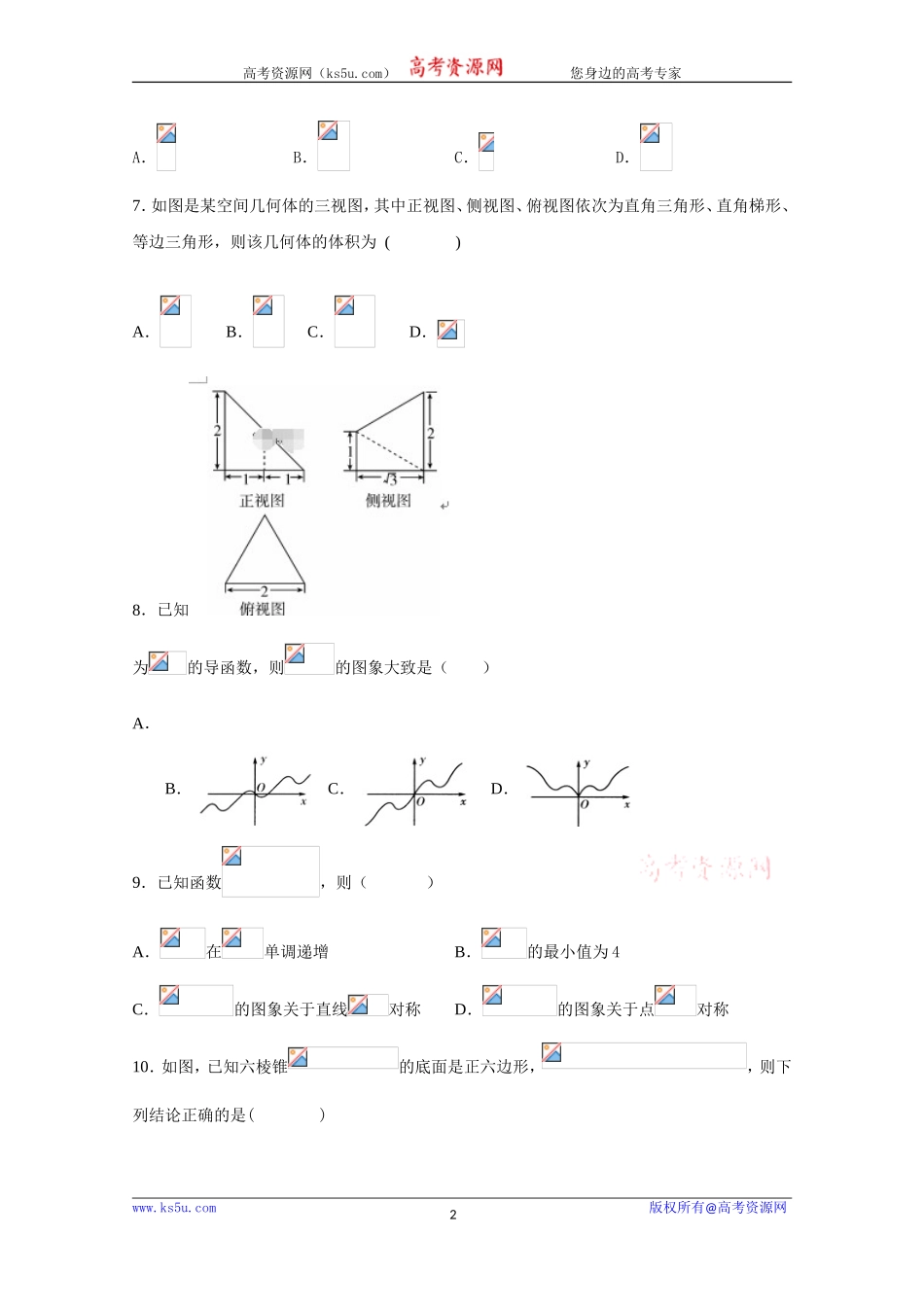
高考资源网(ks5u.com)您身边的高考专家数学(文科)试卷一、选择题(本大题共12小题,每小题5分,共60分)1.已知集合,,,则()A.B.C.D.2.已知复数满足,则复数的共轭复数为()A.B.C.D.3.已知角的顶点与坐标原点重合,始边与轴的非负半轴重合.若点是角终边上一点,则()A.-2B.C.D.24.已知两条平行直线,之间的距离为1,与圆:相切,与相交于,两点,则()A.B.C.3D.5.“”是“,成立”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.若将函数的图象向左平移个单位,得到函数是偶函数,则的最小正值是()www.ks5u.com版权所有@高考资源网1高考资源网(ks5u.com)您身边的高考专家A.B.C.D.7.如图是某空间几何体的三视图,其中正视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积为()A.B.C.D.8.已知为的导函数,则的图象大致是()A.B.C.D.9.已知函数,则()A.在单调递增B.的最小值为4C.的图象关于直线对称D.的图象关于点对称10.如图,已知六棱锥的底面是正六边形,,则下列结论正确的是()www.ks5u.com版权所有@高考资源网2高考资源网(ks5u.com)您身边的高考专家A.B.平面C.直线∥平面D.11.已知数列的前n项和,若不等式,对任意恒成立,则实数m的最小值是()A.B.C.D.12.已知双曲线:的左、右顶点分别为,,点在曲线上,若中,,则双曲线的渐近线方程为()A.B.C.D.二、填空题:(本大题共4小题,每小题5分,共20分.请将答案填写在横线上)13.已知向量,,若,则与夹角的余弦值为______.14.实数x,y满足,则z=4x+3y的最大值为______.15.在平面直角坐标系中,已知圆,圆www.ks5u.com版权所有@高考资源网3高考资源网(ks5u.com)您身边的高考专家,若圆上存在一点,使得以点为圆心,为半径的圆与圆有公共点,则实数的取值范围为________.16.已知,,,,是球的球面上的五个点,四边形为梯形,,,,面,则球的体积为________.三、解答题(本大题共6小题,共70分)17.(本题满分10分)数列中,,.(1)求的通项公式;(2)设,求出数列的前项和.18.(本题满分12分)已知在中,角,,的对边分别为,,,的面积为.(1)求证:;(2)若,求的值.19.(本题满分12分)如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2.www.ks5u.com版权所有@高考资源网4高考资源网(ks5u.com)您身边的高...