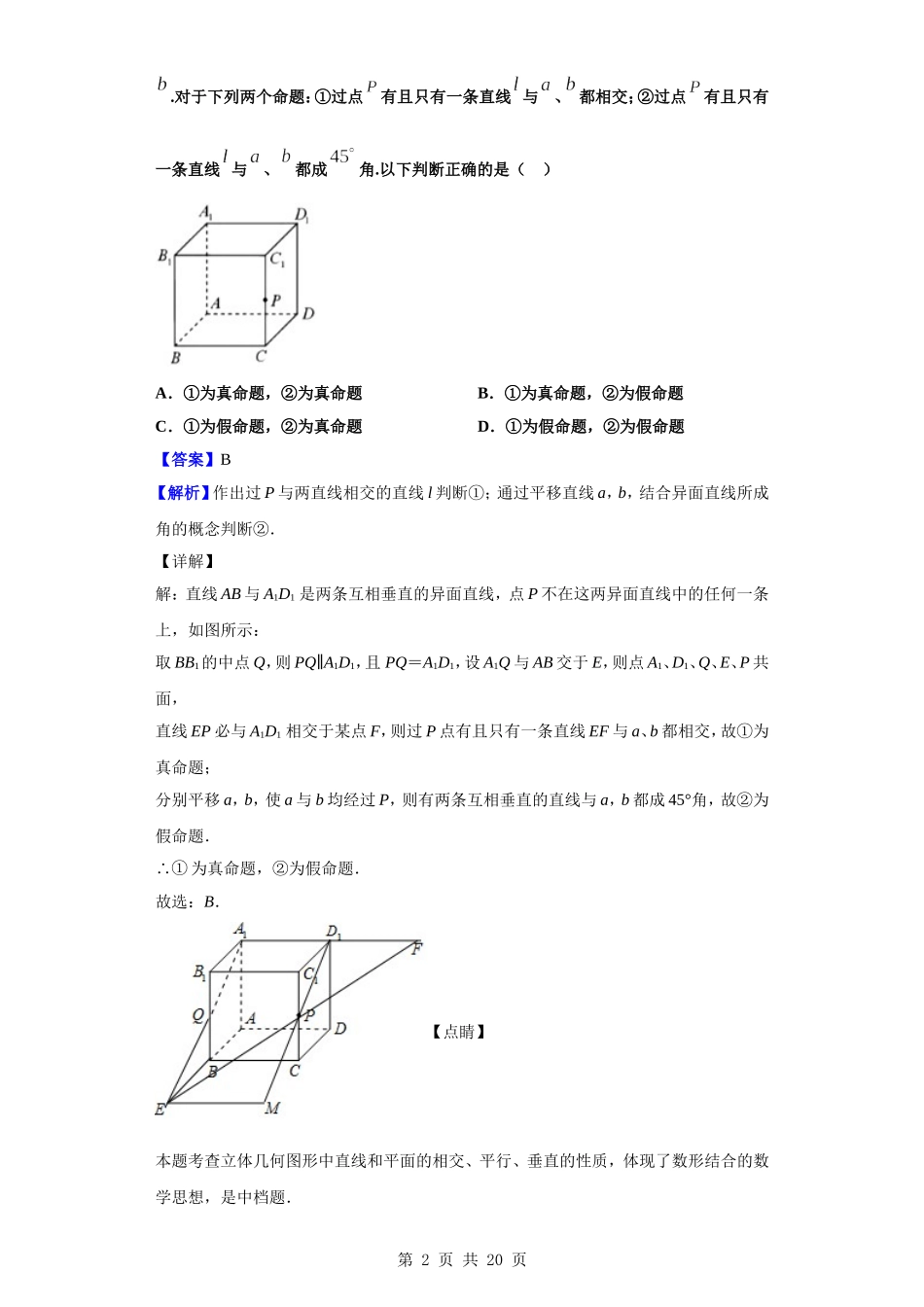
2020届上海市嘉定区、长宁、金山区高三上学期期末数学试题一、单选题1.已知,则“”是“”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件【答案】B【解析】根据充分条件和必要条件的定义分别进行判断即可【详解】解:由题意可知,,⫌“∴”是“”的必要不充分条件.故选:B.【点睛】本题主要考查充分条件和必要条件的判断,是基础题.2.下列函数中,值域为的是()A.B.C.D.【答案】A【解析】由指数函数,幂函数,对数函数及余弦函数的性质直接得解.【详解】解:选项A.的值域为,选项B.的值域为,选项C.的值域为R,选项D.的值域为.故选:A.【点睛】本题考查常见函数的值域,属于简单题.3.已知正方体,点是棱的中点,设直线为,直线为第1页共20页.对于下列两个命题:①过点有且只有一条直线与、都相交;②过点有且只有一条直线与、都成角.以下判断正确的是()A.①为真命题,②为真命题B.①为真命题,②为假命题C.①为假命题,②为真命题D.①为假命题,②为假命题【答案】B【解析】作出过P与两直线相交的直线l判断①;通过平移直线a,b,结合异面直线所成角的概念判断②.【详解】解:直线AB与A1D1是两条互相垂直的异面直线,点P不在这两异面直线中的任何一条上,如图所示:取BB1的中点Q,则PQ∥A1D1,且PQ=A1D1,设A1Q与AB交于E,则点A1、D1、Q、E、P共面,直线EP必与A1D1相交于某点F,则过P点有且只有一条直线EF与a、b都相交,故①为真命题;分别平移a,b,使a与b均经过P,则有两条互相垂直的直线与a,b都成45°角,故②为假命题.∴①为真命题,②为假命题.故选:B.【点睛】本题考查立体几何图形中直线和平面的相交、平行、垂直的性质,体现了数形结合的数学思想,是中档题.第2页共20页4.某港口某天0时至24时的水深(米)随时间(时)变化曲线近似满足如下函数模型().若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为()A.16时B.17时C.18时D.19时【答案】D【解析】本题是单选题,利用回代验证法,结合五点法作图以及函数的最值的位置,判断即可.【详解】解:由题意可知,时,,由五点法作图可知:如果当时,函数取得最小值可得:,可得,此时函数,函数的周期为:,该港口在该天0时至24时内,有且只有3个时刻水深为3米,满足,如果当时,函数取得最小值可得:,可得,此时函数,函数的周期为:,时,,如图:该港口在该天0时至24时内,有且...