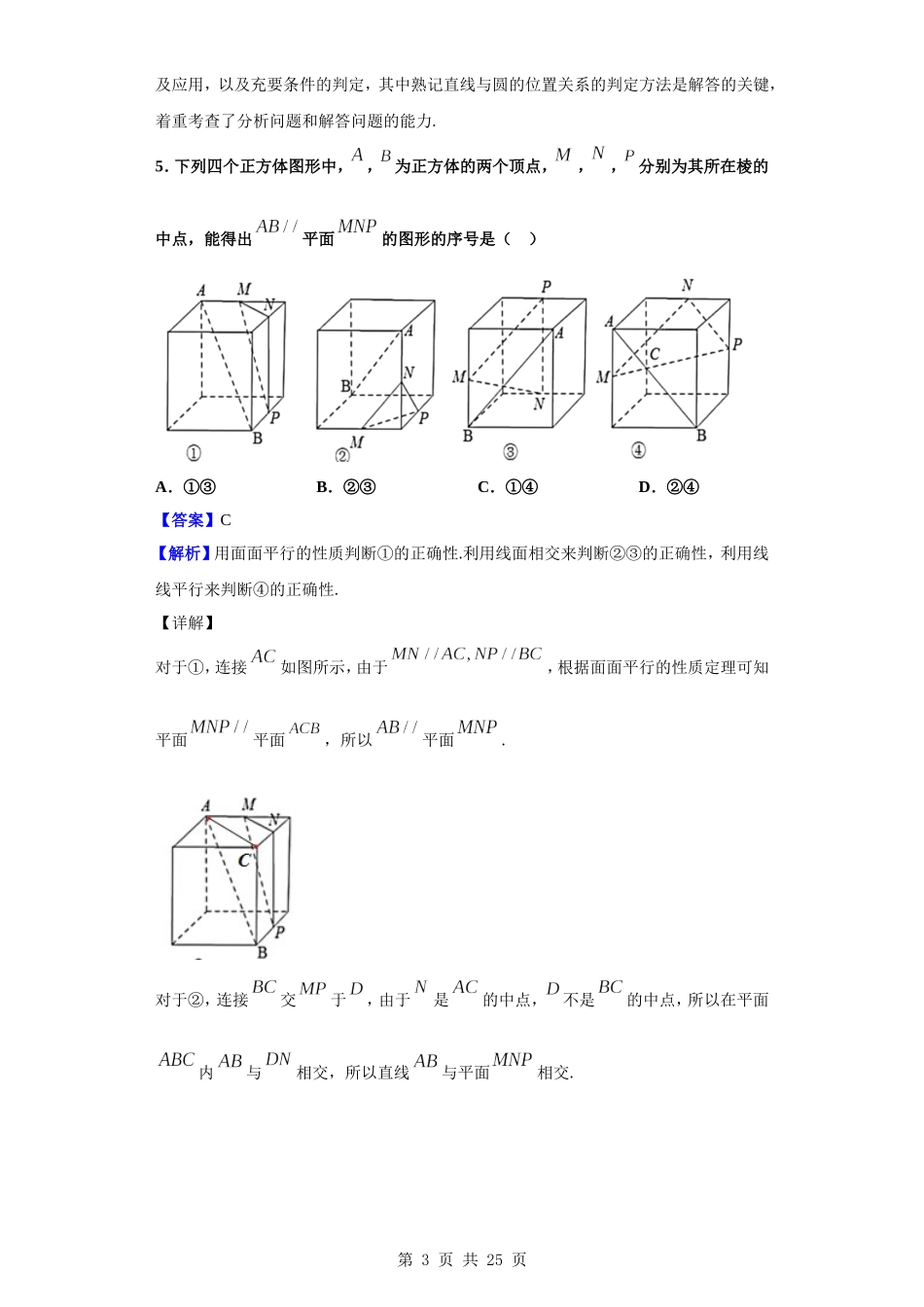
2020届广东省中山市高三上学期期末数学(文)试题一、单选题1.集合,,则()A.B.C.D.【答案】D【解析】由题意得,∴.选D.2.已知是虚数单位,复数满足,则()A.B.C.D.5【答案】A【解析】利用复数乘法和除法运算求得,进而求得的模.【详解】依题意,所以.故选:A【点睛】本小题主要考查复数乘法和除法运算,考查复数的模的计算,属于基础题.第1页共25页3.计算的结果为()A.B.C.D.【答案】B【解析】根据诱导公式,化简三角函数值;再根据正弦的差角公式合并即可得到解。【详解】所以选B【点睛】本题考查了三角函数诱导公式、正弦差角公式的简单应用,属于基础题。4.“”是直线与圆相切的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C【解析】由圆的方程得到圆心坐标和半径,使得圆心到直线的距离等于圆的半径,得到的值,即可得到结论.【详解】由圆,可得圆心为,半径. 直线与圆相切,∴,∴,∴“”是直线与圆相切的充要条件,故选C.【点睛】本题主要考查了充要条件的判定及应用,其中解答中涉及到直线与圆的位置关系的判定第2页共25页及应用,以及充要条件的判定,其中熟记直线与圆的位置关系的判定方法是解答的关键,着重考查了分析问题和解答问题的能力.5.下列四个正方体图形中,,为正方体的两个顶点,,,分别为其所在棱的中点,能得出平面的图形的序号是()A.①③B.②③C.①④D.②④【答案】C【解析】用面面平行的性质判断①的正确性.利用线面相交来判断②③的正确性,利用线线平行来判断④的正确性.【详解】对于①,连接如图所示,由于,根据面面平行的性质定理可知平面平面,所以平面.对于②,连接交于,由于是的中点,不是的中点,所以在平面内与相交,所以直线与平面相交.第3页共25页对于③,连接,则,而与相交,即与平面相交,所以与平面相交.对于④,连接,则,由线面平行的判定定理可知平面.综上所述,能得出平面的图形的序号是①④.故选:C【点睛】本小题主要考查线面平行的判定,考查空间想象能力和逻辑推理能力,属于基础题.6.若,则()A.B.C.D.【答案】D【解析】分析:三个对数的底数和真数的比值都是,因此三者可化为的形第4页共25页式,该函数为上的单调增函数,从而得到三个对数的大小关系.详解:,,,令,则在上是单调增函数.又,所以即.故选D.点睛:对数的大小比较,要观察不同对数的底数和真数的关系,还要关注对数本身的底数与真数的关系,从而找...