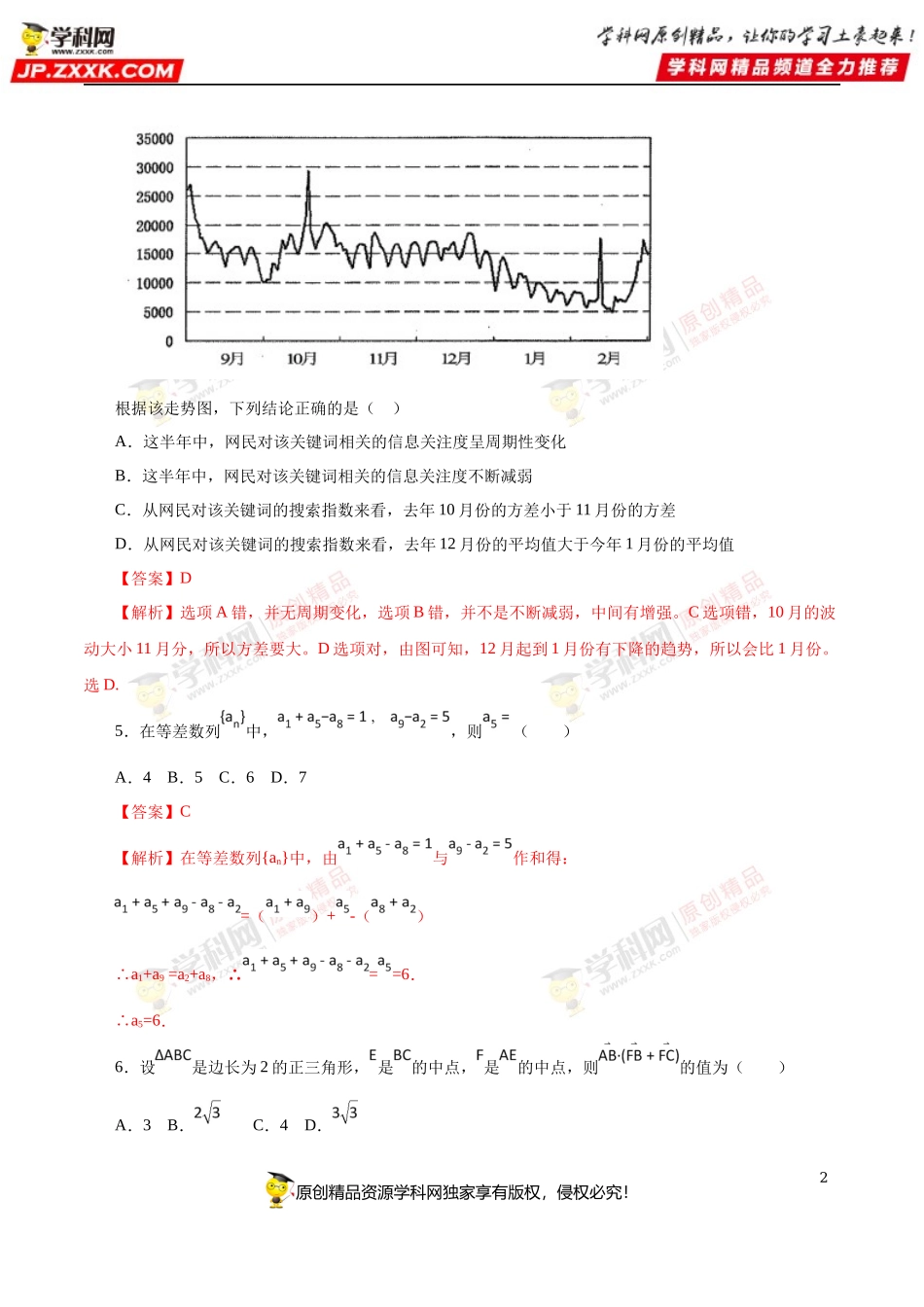
1原创精品资源学科网独家享有版权,侵权必究!2019黄金押题三一、选择题1.设集合,,则()A.B.C.D.【答案】B【解析】A={x|y=log2(2x﹣)}={x|x<2},B={x|x23x+2﹣<0}={x|1<x<2},则∁AB={x|x≤1},故选:B.2.已知复数z满足,则A.B.1C.D.5【答案】C【解析】由题意,。3.已知,,,(为自然对数的底数),则()A.B.C.D.【答案】B【解析】,,,则4.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高。下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图。2原创精品资源学科网独家享有版权,侵权必究!根据该走势图,下列结论正确的是()A.这半年中,网民对该关键词相关的信息关注度呈周期性变化B.这半年中,网民对该关键词相关的信息关注度不断减弱C.从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差D.从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值【答案】D【解析】选项A错,并无周期变化,选项B错,并不是不断减弱,中间有增强。C选项错,10月的波动大小11月分,所以方差要大。D选项对,由图可知,12月起到1月份有下降的趋势,所以会比1月份。选D.5.在等差数列中,,则()A.4B.5C.6D.7【答案】C【解析】在等差数列{an}中,由与作和得:=()+-()a∴1+a9=a2+a8,∴==6.a∴5=6.6.设是边长为2的正三角形,是的中点,是的中点,则的值为()A.3B.C.4D.3原创精品资源学科网独家享有版权,侵权必究!【答案】A【解析】,故选A.7.已知抛物线的焦点为,点为上一动点,,,且的最小值为,则等于()A.B.5C.D.4【答案】C【解析】设,则因为,所以或(舍去).所以8.已知,则的值为A.B.C.D.4原创精品资源学科网独家享有版权,侵权必究!【答案】B【解析】。9.一个空间几何体的三视图如图所示,俯视图为正三角形,则它的外接球的表面积为()A.B.C.D.【答案】B【解析】由三视图可知还几何体是以为底面的四棱锥,过作,垂足为,易证面,设其外接球半径为,底面ABCD是正方形外接圆,.设圆心与球心的距离为,则由此可得,故其外接球的表面积故选B.10.已知直三棱柱的底面为等边三角形,且底面积为,体积为,点,分别为线段5原创精品资源学科网独家享有版权,侵权必究!,上的动点,若直线平面,点为线段的中点...