【全国百强校word】河北省衡水中学2018届高三高考押题(二）理数试题.doc

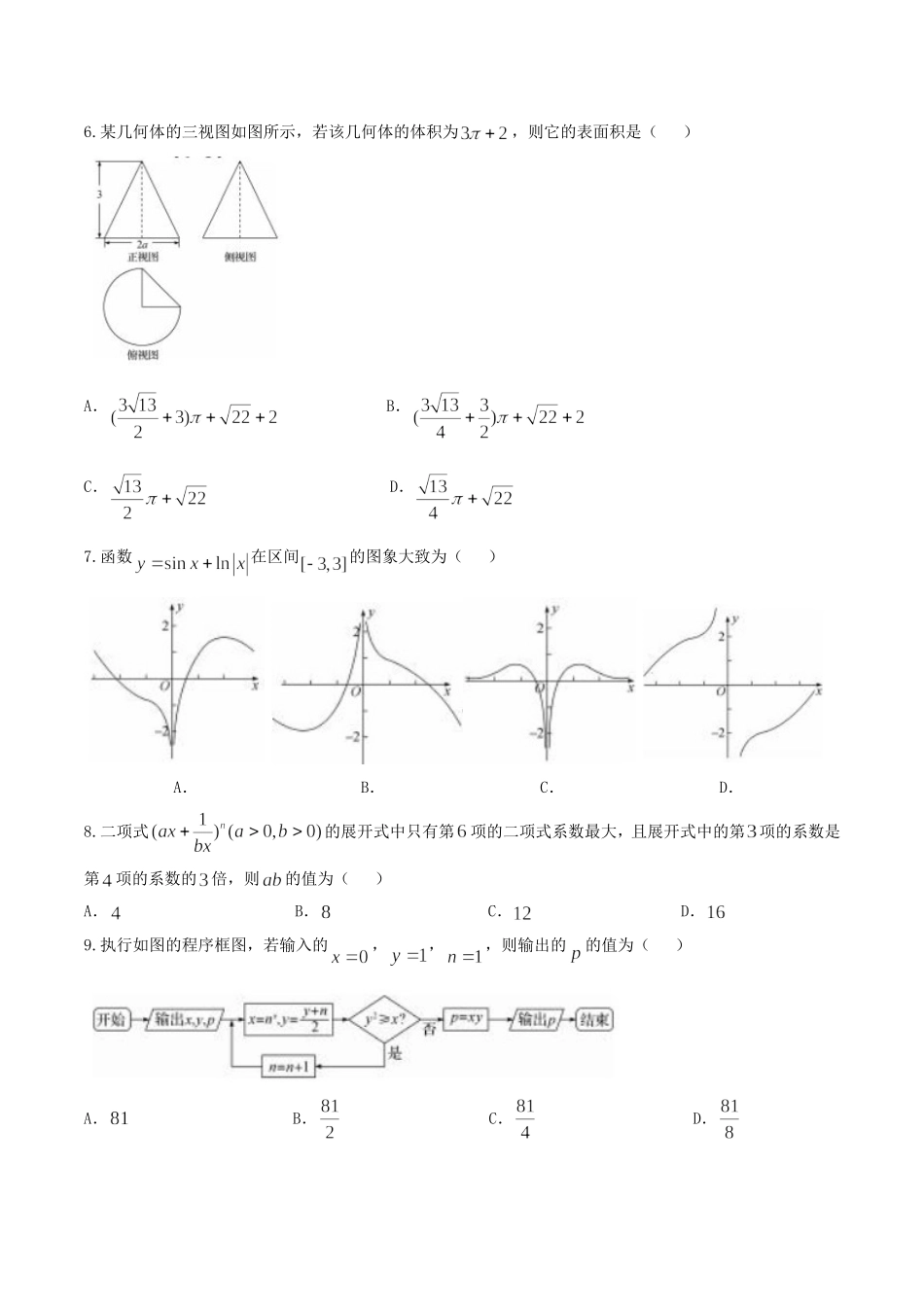
河北衡水中学2018年高考押题试卷 理数试卷（二） 第Ⅰ卷 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.设集合，，则（ ） A． B． C． D． 2.设复数满足，则（ ） A． B． C． D． 3.若，，则的值为（ ） A． B． C． D． 4.已知直角坐标原点为椭圆：的中心，，为左、右焦点，在区间任取一个数，则事件“以为离心率的椭圆与圆：没有交点”的概率为（ ） A． B． C． D． 5.定义平面上两条相交直线的夹角为：两条相交直线交成的不超过的正角.已知双曲线：，当其离心率时，对应双曲线的渐近线的夹角的取值范围为（ ） A． B． C． D． 6.某几何体的三视图如图所示，若该几何体的体积为，则它的表面积是（ ） A． B． C． D． 7.函数在区间的图象大致为（ ） A． B． C． D． 8.二项式的展开式中只有第项的二项式系数最大，且展开式中的第项的系数是第项的系数的倍，则的值为（ ） A． B． C． D． 9.执行如图的程序框图，若输入的，，，则输出的的值为（ ） A． B． C． D． 10.已知数列，，且，，则的值为（ ） A． B． C． D． 11.已知函数的图象如图所示，令，则下列关于函数的说法中不正确的是（ ） A．函数图象的对称轴方程为 B．函数的最大值为 C．函数的图象上存在点，使得在点处的切线与直线：平行 D．方程的两个不同的解分别为，，则最小值为 12.已知函数，若存在三个零点，则的取值范围是（ ） A． B． C． D． 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分. 13.向量，，若向量，共线，且，则的值为 ． 14.设点是椭圆上的点，以点为圆心的圆与轴相切于椭圆的焦点，圆与轴相交于不同的两点、，若为锐角三角形，则椭圆的离心率的取值范围为 ． 15.设，满足约束条件，则的取值范围为 ． 16.在平面五边形中，已知，，，，，，当五边形的面积时，则的取值范围为 ． 三、解答题：解答应写出文字说明、证明过程或演算步骤. 17.已知数列的前项和为，，. （1）求数列的通项公式； （2）记，求的前项和. 18.如图所示的几何体中，底面为菱形，，，与相交于点，四边形为直角梯形，，，，平面底面. （1）证明：平面平面； （2）求二面角的余弦值. 19.某校为缓解高三学生的高考压力，经常举行一些心理素质综合能力训练活动，经过一段时间的训练后从该年级名学生中随机抽取名学生进行测试，并将其成绩分为、、、、五个等级，统计数据如图所示（视频率为概率），根据以上抽样调查数据，回答下列问题： （1）试估算该校高三年级学生获得成绩为的人数； （2）若等级、、、、分别对应分、分、分、分、分，学校要求平均分达分以上为“考前心理稳定整体过关”，请问该校高三年级目前学生的“考前心理稳定整体”是否过关？ （3）为了解心理健康状态稳定学生的特点，现从、两种级别中，用分层抽样的方法抽取个学生样本，再从中任意选取个学生样本分析，求这个样本为级的个数的分布列与数学期望. 20.已知椭圆：的离心率为，且过点，动直线：交椭圆于不同的两点，，且（为坐标原点）. （1）求椭圆的方程. （2）讨论是否为定值？若为定值，求出该定值，若不是请说明理由. 21.设函数. （1）试讨论函数的单调性； （2）设，记，当时，若方程有两个不相等的实根，，证明. 请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分，作答时请写清题号. 22.选修4-4：坐标系与参数方程 在直角坐标系中，曲线：（为参数，），在以坐标原点为极点，轴的非负半轴为极轴的极坐标系中，曲线：. （1）试将曲线与化为直角坐标系中的普通方程，并指出两曲线有公共点时的取值范围； （2）当时，两曲线相交于，两点，求. 23.选修4-5：不等式选讲 已知函数. （1）在下面给出的直角坐标系中作出函数的图象，并由图象找出满足不等式的解集； （2）若函数的最小值记为，设，且有，试证明：. 参考答案及解析 理科数学（Ⅱ） 一、选择题 1-5: BCAAD 6-10: AABCC 11、12：CD 二、填空题 13. 14. 15. 16. 三、解答题 17.解：（1）当时，由及， 得，即，解得. 又由，① 可知，② ②-①得，即. 且时，适合上式，因此数列是以为首项，为公比的等比数列，故. （2）由（1）及， 可知， 所以， 故. 18.解：（1）因为底面为菱形，所以， 又平面底面，平面平面， 因此平面，从而. 又，所以平面， 由，，， 可知，， ，， 从而，故. 又，所以平面. 又平面，所以平面平面. （2）取中点，由题可知，所以平面，又在菱形中，，所以分别以，，的方向为，，轴正方向建立空间直角坐标系（如图示）， 则，，，，， 所以， ，. 由（1）可知平面，所以平面的法向量可取为. 设平面的法向量为， 则，即，即，令，得， 所以. 从而. 故所求的二面角的余弦值为. 19.解：（1）从条形图中可知这人中，有名学生成绩等级为， 所以可以估计该校学生获得成绩等级为的概率为， 则该校高三年级学生获得成绩为的人数约有. （2）这名学生成绩的平均分为， 因为，所以该校高三年级目前学生的“考前心理稳定整体”已过关. （3）由题可知用分层抽样的方法抽取个学生样本，其中级个，级个，从而任意选取个，这个为级的个数的可能值为，，，. 则，， ，. 因此可得的分布列为： 则. 20.解：（1）由题意可知，所以，即，① 又点在椭圆上，所以有，② 由①②联立，解得，， 故所求的椭圆方程为. （2）设，，由， 可知. 联立方程组， 消去化简整理得， 由，得，所以，，③ 又由题知， 即， 整理为. 将③代入上式，得. 化简整理得，从而得到. 21.解：（1）由，可知. 因为函数的定义域为，所以， ①若时，当时，，函数单调递减，当时，，函数单调递增； ②若时，当在内恒成立，函数单调递增； ③若时，当时，，函数单调递减，当时，，函数单调递增. （2）证明：由题可知， 所以. 所以当时，；当时，；当时，. 欲证，只需证，又，即单调递增，故只需证明. 设，是方程的两个不相等的实根，不妨设为， 则， 两式相减并整理得， 从而， 故只需证明， 即. 因为， 所以式可化为， 即. 因为，所以， 不妨令，所以得到，. 设，，所以，当且仅当时，等号成立，因此在单调递增. 又， 因此，， 故，得证， 从而得证. 22.解：（1）曲线：，消去参数可得普通方程为. 曲线：，两边同乘.可得普通方程为. 把代入曲线的普通方程得：， 而对有，即，所以故当两曲线有公共点时，的取值范围为. （2）当时，曲线：， 两曲线交点，所在直线方程为. 曲线的圆心到直线的距离为， 所以. 23.解：（1）因为， 所以作出图象如图所示，并从图可知满足不等式的解集为. （2）证明：由图可知函数的最小值为，即. 所以，从而， 从而 . 当且仅当时，等号成立， 即，时，有最小值， 所以得证.