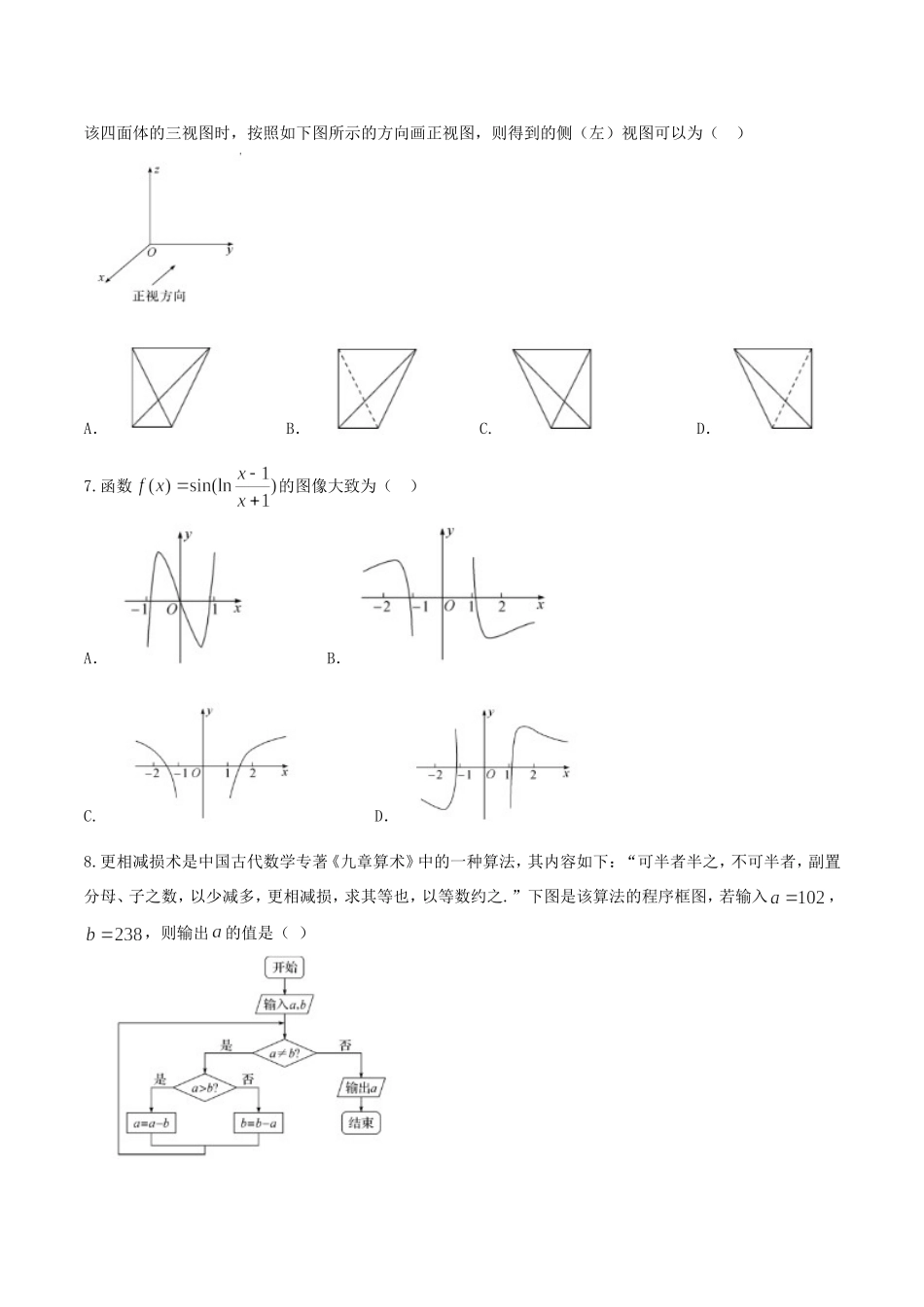
2017-2018学年度上学期高三年级七调考试数学(理科)试卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,,全集,若,则有()A.B.C.D.2.若复数满足(为虚数单位),则的虚部是()A.-2B.4C.D.-43.已知,,,成等差数列,,,,,成等比数列,则的值是()A.B.C.或D.4.如图,5个数据,去掉后,下列说法错误的是()A.相关系数变大B.残差平方和变大C.相关指数变大D.解释变量与预报变量的相关性变强5.已知,分别是椭圆的左、右焦点,若椭圆上存在点,使,则该椭圆的离心率的取值范围为()A.B.C.D.6.一个四面体的顶点在空间直角坐标系中的坐标分别是,,,,绘制该四面体的三视图时,按照如下图所示的方向画正视图,则得到的侧(左)视图可以为()A.B.C.D.7.函数的图像大致为()A.B.C.D.8.更相减损术是中国古代数学专著《九章算术》中的一种算法,其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之.”下图是该算法的程序框图,若输入,,则输出的值是()A.68B.17C.34D.369.已知为自然对数的底数,若对任意的,总存在唯一的,使得成立,则实数的取值范围是()A.B.C.D.10.电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:电视台每周安排的甲、乙连续剧的总播放时长不多于,广告的总播放时长不少于,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍,分别用,表示每周计划播出的甲、乙两套连续剧的次数,要使总收视人次最多,则电视台每周播出甲、乙两套连续剧的次数分别为()A.6,3B.5,2C.4,5D.2,711.已知在正四面体中,是棱的中点,是点在底面内的射影,则异面直线与所成角的余弦值为()A.B.C.D.12.已知,,其中,若函数在区间内没有零点,则的取值范围是()A.B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.如图,在半径为2的扇形中,,为弧上的一点,若,则的值为.14.若从区间(为自然对数的底数,)内随机选取两个数,则这两个数之积小于的概率为.15.已知在中,角,,的对边分别为,,,则下列四个论断中正确的是.(把你认为是正确论断的序号都写上)①若,则;②若,,,则满足条件的三角形共有两个;③若,,成等差数列,,,成等比数列,则为正三角...