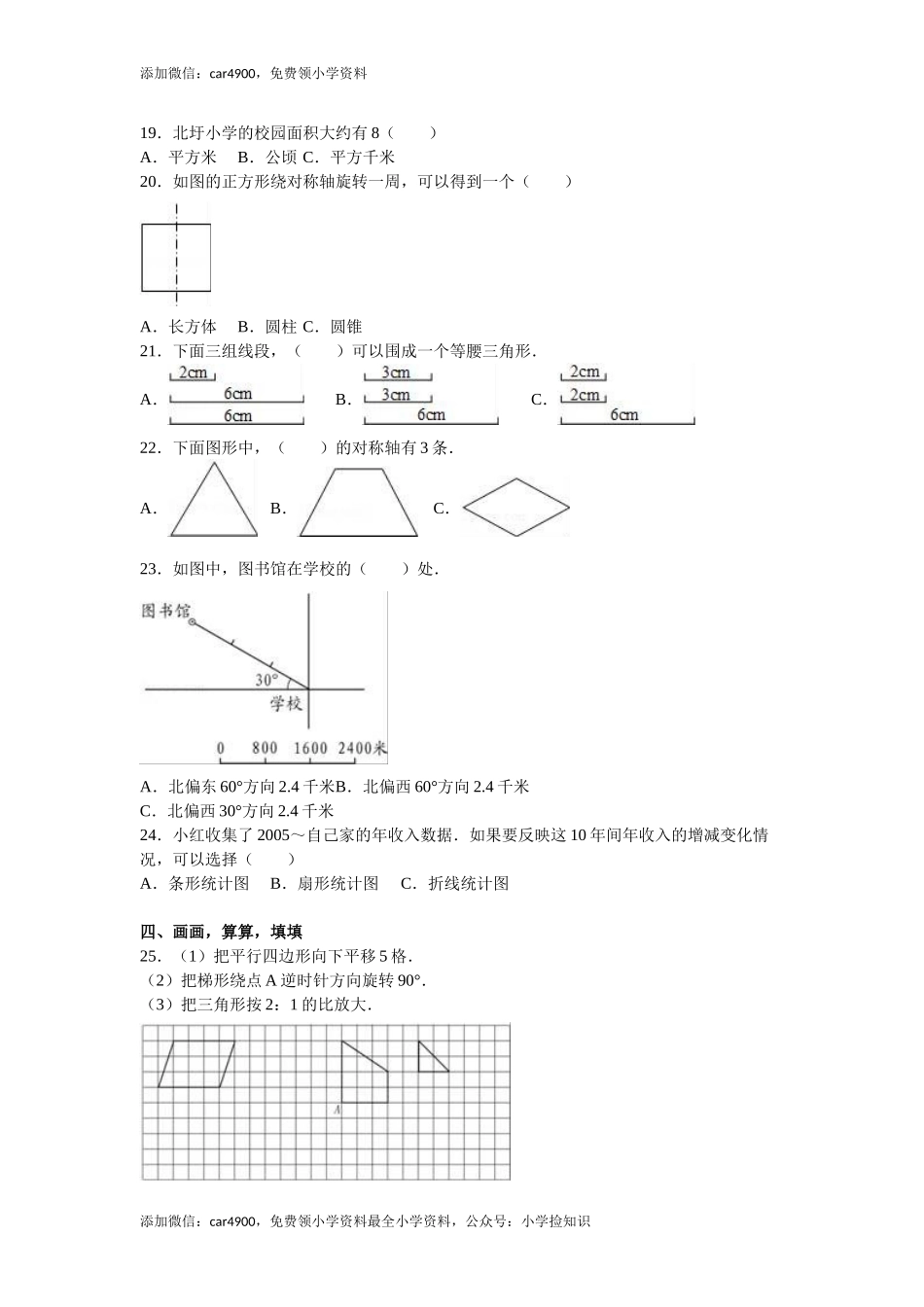
添加微信:car4900,免费领小学资料苏教版数学六年级下学期期末测试卷一、计算1.直接写出得数.25+69=0.720.58=﹣0.2÷0.001=0.8×1.2×1.25=+=×=÷=+++=2.下面各题,能简便计算的用简便方法计算.(9.72.154.85﹣﹣)÷0.9×++÷[﹣(+)](11×﹣)÷.4.解方程.1.8x5.9=3.1﹣;x+x=7;5:x=:.二、填空添加微信:car4900,免费领小学资料最全小学资料,公众号:小学捡知识添加微信:car4900,免费领小学资料5.,某市实现生产总值二百七十亿零六百万元,横线上的数写作:,“四舍五入”到“亿”位大约是亿元.6.时=分;5020立方厘米=立方分米.7.5÷8==15:=%.8.1~20的数中,既是2的倍数又是3的倍数的有,既是3的倍数又是5的倍数的有.9.吨是1吨的,是3吨的.10.东沟村今年种植柳树与梧桐树棵数的比是5:8,种植柳树的棵数是梧桐树的%,种植梧桐树的棵数是柳树的%.11.一个直角三角形的一个锐角是43°,它的另一个锐角是.12.冬冬用1立方厘米小正方体摆长方体,从前、右和上看到的形状如图:这个长方体的表面积是平方厘米,体积是立方厘米.13.把一个半径8厘米的圆平均分成32份,再拼成一个近似的长方形.拼成长方形的长是厘米,面积是平方厘米.14.学校航模组制作了一架摇控飞机,下面是这架飞机前6次试飞情况记录:次数123456飞行距离/m323826554358这架飞机前6次平均飞行距离是米.如果第7次试飞的距离是49米,前7次的平均飞行距离是米.三、选择合适答案的序号填在括号里15.下面的三道算式中,()的得数不可能超过3.6.A.4.08×0.92B.4.08×0.89C.3.98×0.8916.已知a是b的.下面的三句话中,()是错误的.A.a比b少B.b比a多C.b比a多17.下面的三句话中,()是正确的.A.今年的水稻比去年增产一成,表示今年的水稻比去年增产10%B.一种商品打六折出售,就是按原价的6%出售C.在100克水中加入2克盐,这种盐水的含盐率是2%18.下面各题,()中的两种量成反比例关系.A.汽车的速度一定,行驶的时间和路程B.购买商品的数量一定,商品的单价和总价C.三角形的面积一定,它的底和高添加微信:car4900,免费领小学资料最全小学资料,公众号:小学捡知识添加微信:car4900,免费领小学资料19.北圩小学的校园面积大约有8()A.平方米B.公顷C.平方千米20.如图的正方形绕对称轴旋转一周,可以得到一个()A.长方体B.圆柱C.圆锥21.下面三组线段,()可以围成一个等腰三角形.A.B.C.22.下面图形中,()的对...