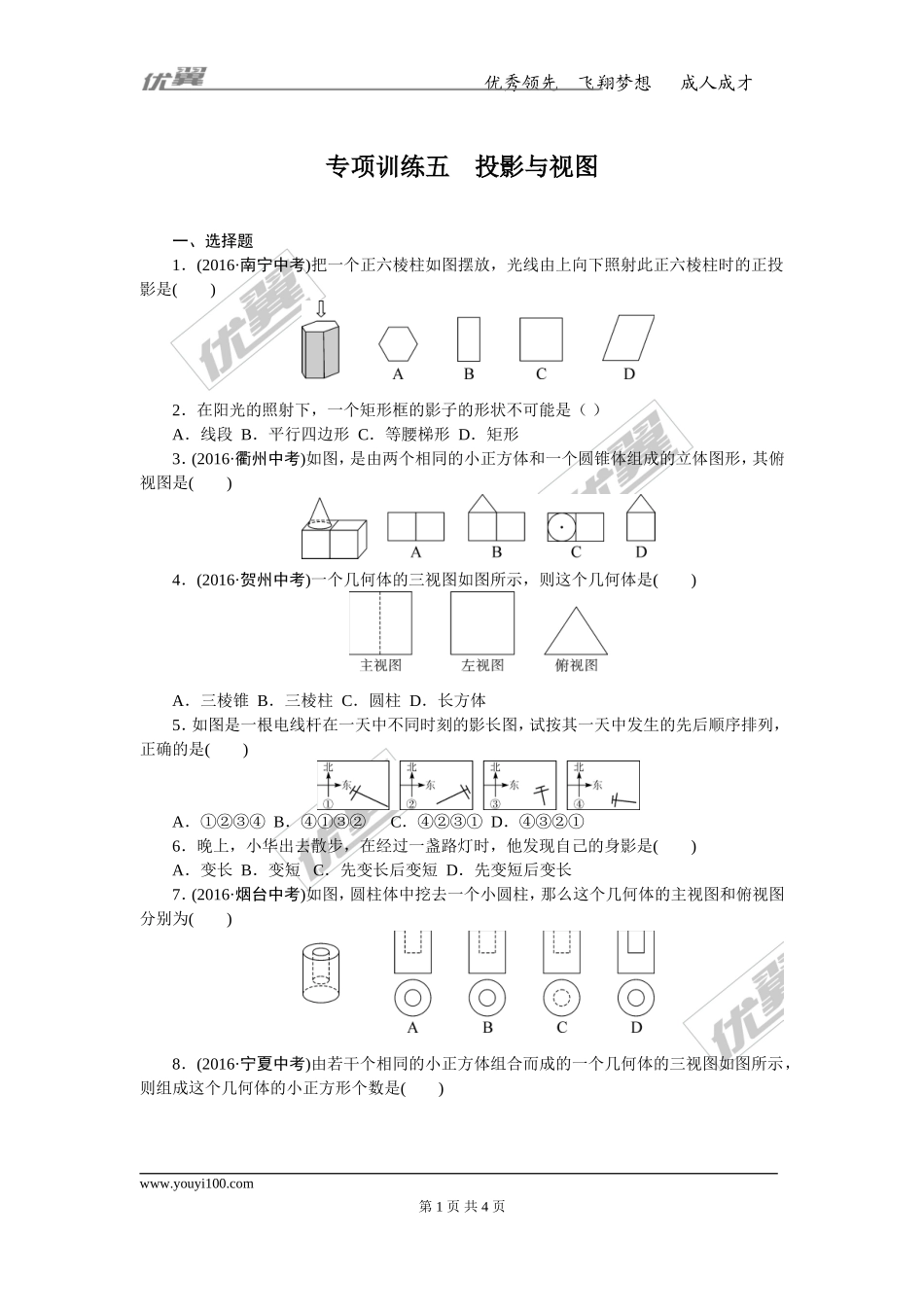
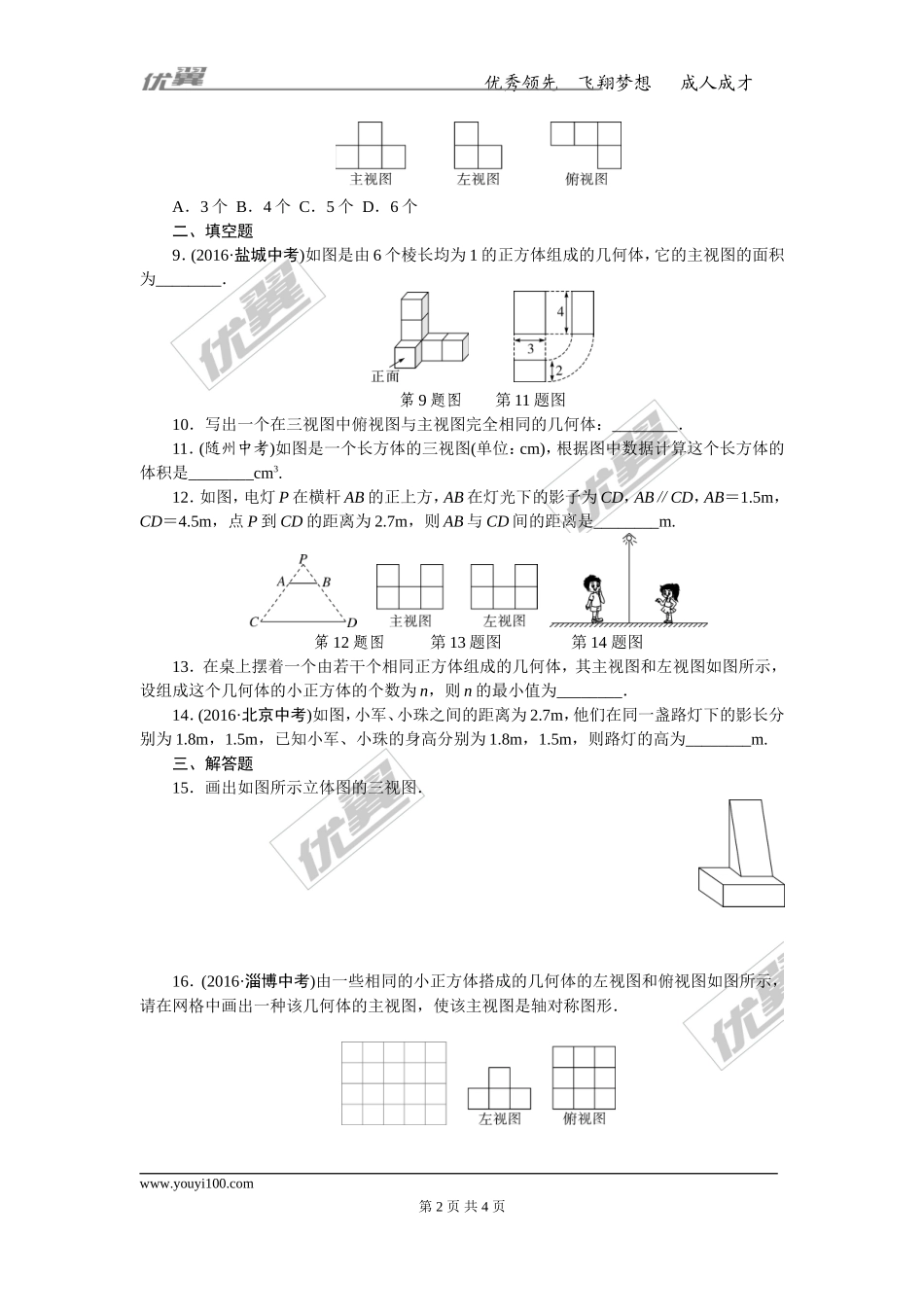
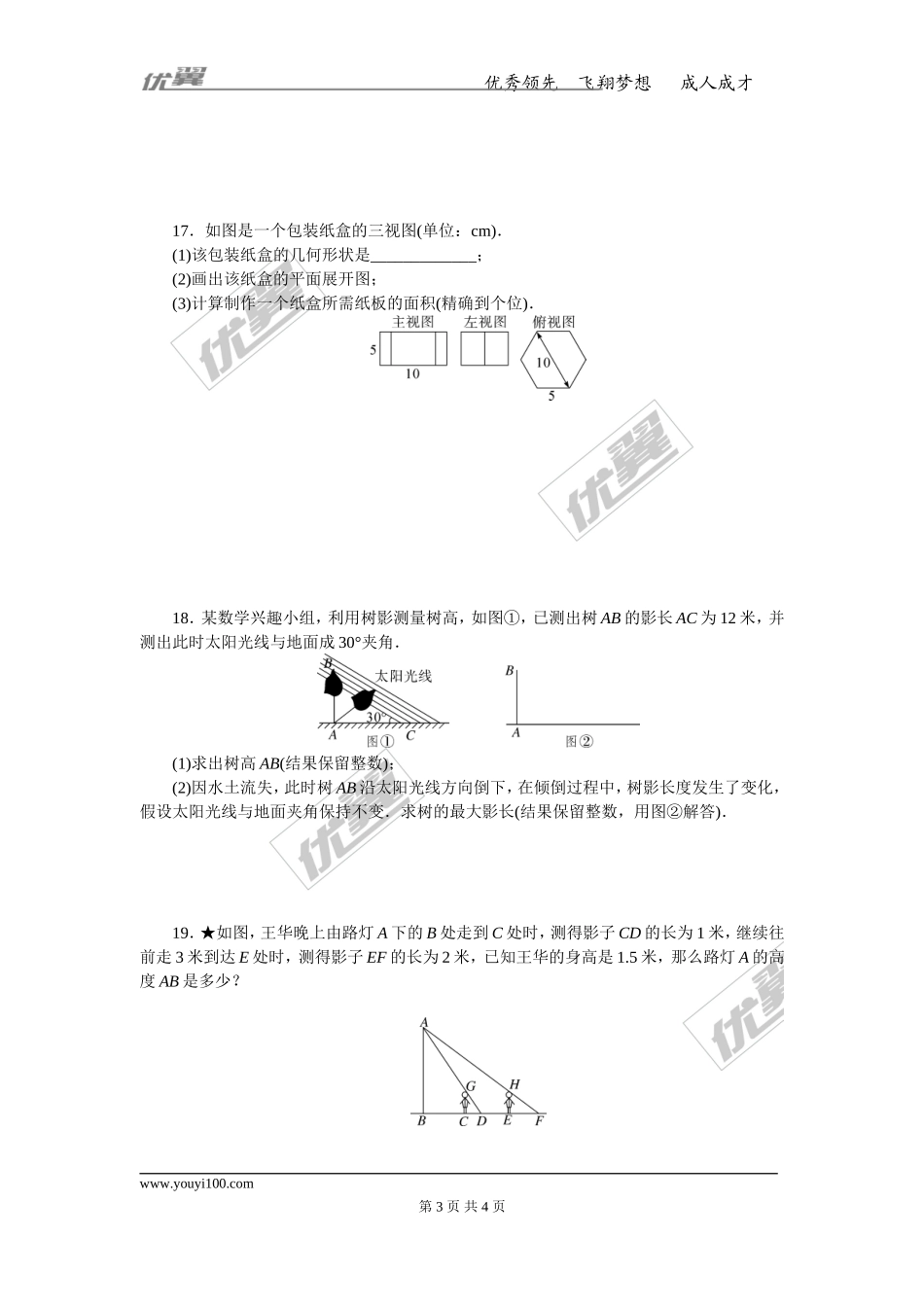
优秀领先飞翔梦想成人成才专项训练五投影与视图一、选择题1.(2016·南宁中考)把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是()2.在阳光的照射下,一个矩形框的影子的形状不可能是()A.线段B.平行四边形C.等腰梯形D.矩形3.(2016·衢州中考)如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,其俯视图是()4.(2016·贺州中考)一个几何体的三视图如图所示,则这个几何体是()A.三棱锥B.三棱柱C.圆柱D.长方体5.如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是()A.①②③④B.④①③②C.④②③①D.④③②①6.晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影是()A.变长B.变短C.先变长后变短D.先变短后变长7.(2016·烟台中考)如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为()8.(2016·宁夏中考)由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方形个数是()www.youyi100.com第1页共4页优秀领先飞翔梦想成人成才A.3个B.4个C.5个D.6个二、填空题9.(2016·盐城中考)如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为________.第9题图第11题图10.写出一个在三视图中俯视图与主视图完全相同的几何体:________.11.(随州中考)如图是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是________cm3.12.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=1.5m,CD=4.5m,点P到CD的距离为2.7m,则AB与CD间的距离是________m.第12题图第13题图第14题图13.在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为________.14.(2016·北京中考)如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.三、解答题15.画出如图所示立体图的三视图.16.(2016·淄博中考)由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中画出一种该几何体的主视图,使该主视图是轴对称图形.www.youyi100.com第2页共4页优秀领先飞翔梦想成人成才17.如图是一个包装纸盒的三视图(单位:cm).(1)该包装纸盒的几何形状是_____________;(2)画出该纸盒的平面展开图;(3)计算制作一...