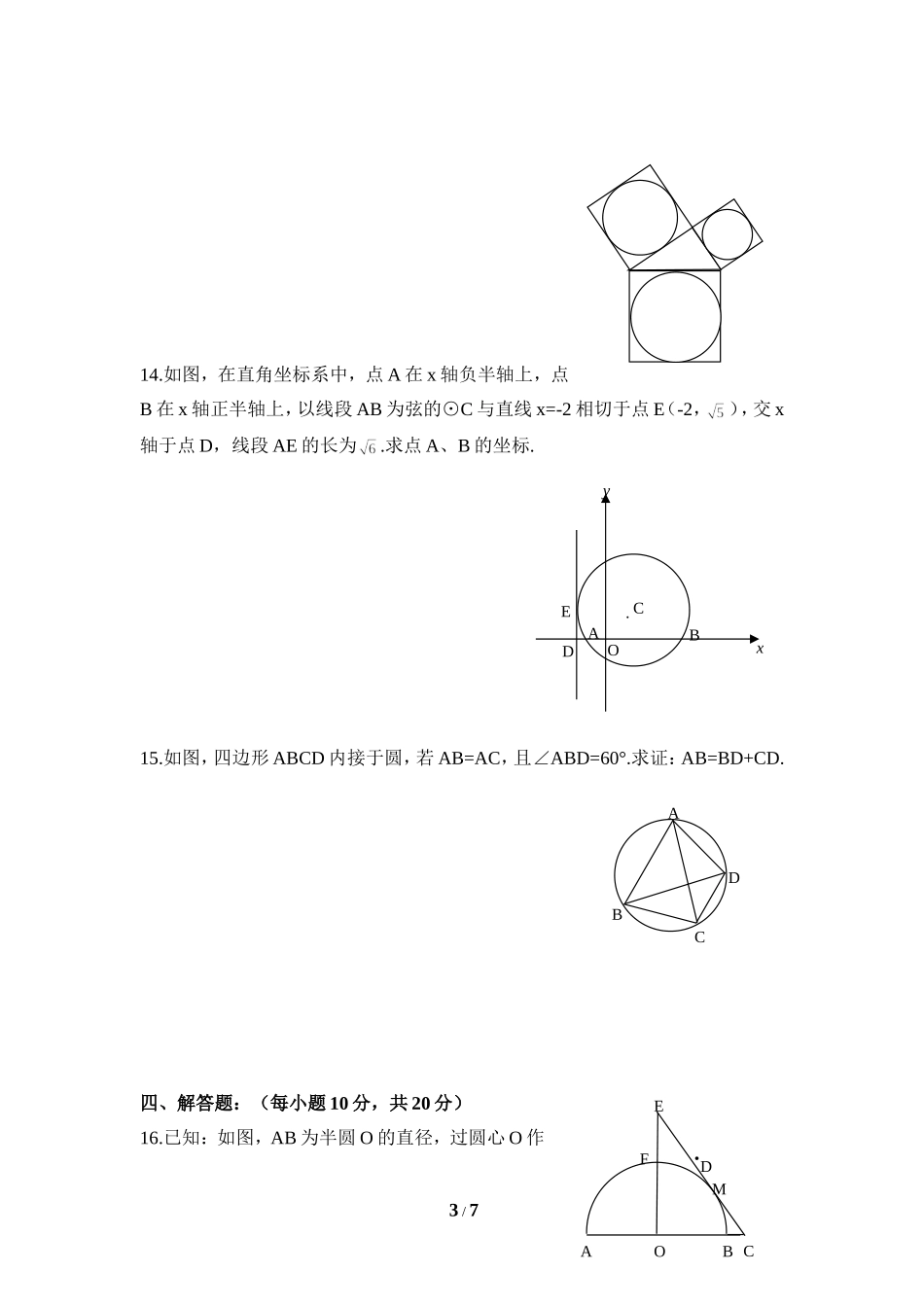
第三章圆单元测试一、选择题:(每小题4分,共20分)1.⊙O的直径是15cm,CD经过圆心O,与⊙O交于C、D两点,垂直弦AB于M,且OM:OC=3:5,则AB=()A.24cmB.12cmC.6cmD.3cm2.⊙O的直径是3,直线与⊙O相交,圆心O到直线的距离是d,则d应满足()A.d>3B.1.5r),圆心距为d,且R2+d2-r2=2Rd,则这两圆的位置关系是()A.内含B.相切C.相交D.相离4.若直径为4cm,6cm的两个圆相外切,那么与这两个圆都相切且半径为5cm的圆的个数是()A.5个B.4个C.3个D.2个5.圆内接正方形与该圆的内接正六边形的周长比为()A.2:3B.:C.:2D.2:3二、填空题:(每小题4分,共20分)6.过⊙O内一点P的最长的弦是10cm,最短的弦是8cm,则OP和长为cm.7.如图,弦AC,BD相交于E,并且,∠BEC=110°,则∠ACD的度数是.8.若三角形的周长为9,面积为S,其内切圆的半径为r,则r:S=.9.已知∠AOB=30°,M为OB边上一点,以M为圆心,2cm为半径作⊙M与OA相切,切点为N,则△MON的面积为.1/7ABCDE第7题10.如图①是半径为1的圆,在其中挖去2个半径为的圆得到图②,挖去22个半径为()2的圆得到图③……,则第n(n>1)个图形阴影部分的面积是.……三、解答题:(每小题8分,共40分)11.如图,AB是⊙O的直径,CF⊥AB交⊙O于E、F,连结AC交⊙O于D.求证:CD·AD=DE·DF.12.用钢丝制作两个不同的轴对称模型,如下图,这两个模型中大圆半径都是1米,模型甲中大圆内连接两个等边三角形,模型乙中大中圆内连接两个正方形.这两个图案哪个用料多一点?为什么?13.如图,分别以Rt△ABC的三边向外作正方形,然后分别作三个正方形的内切圆试探究三个圆的面积之间的关系.2/7图①图②图③AFBECDO·模型甲模型乙14.如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,),交x轴于点D,线段AE的长为.求点A、B的坐标.15.如图,四边形ABCD内接于圆,若AB=AC,且∠ABD=60°.求证:AB=BD+CD.四、解答题:(每小题10分,共20分)16.已知:如图,AB为半圆O的直径,过圆心O作3/7FEDM·AOBCADEOBxy·CABCDEO⊥AB,交半圆于F,过E作EC切⊙O于M,交AB的延长线于C,在EC上取一点D,使CD=OC,请你判断DF与⊙O有什么关系,并证明你的判断的正确性.17.如图,正三角形ABC的中心O恰好为扇形ODE的圆心,且点B在扇形内,要使扇形ODE绕点O无论怎样转动,△ABC与扇形重叠部分的面积总等于△ABC的面积的,扇...