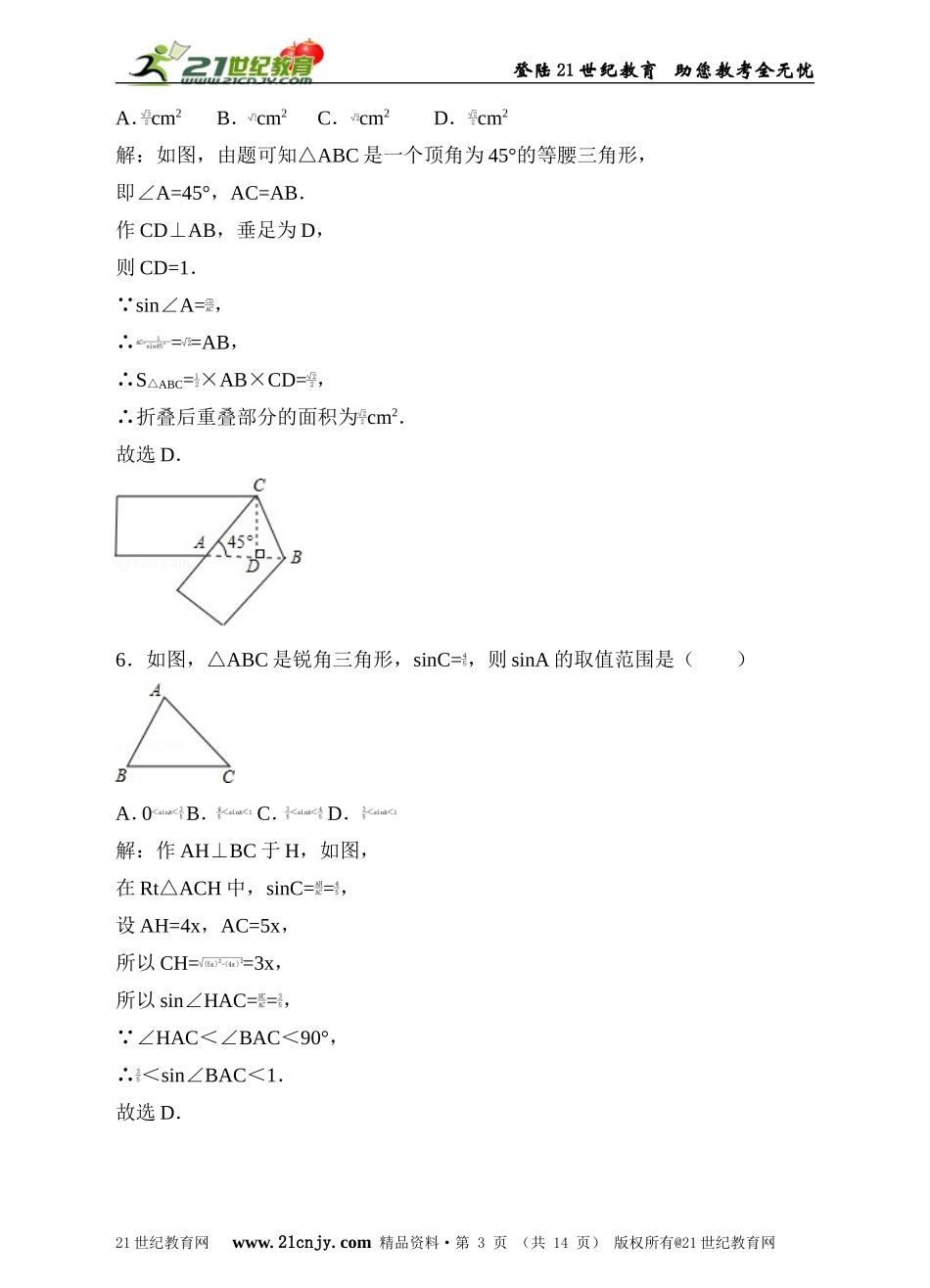
登陆21世纪教育助您教考全无忧北师大版九年级下册期中考试数学试卷参考答案与试题解析一.选择题(共12小题,每小题3分,满分36分)题号123456789101112答案DBCBDDCDDBDC解析:1.在△ABC中,∠C=90°,AB=5,BC=4,那么∠A的正弦值是()A.B.C.D.解: ∠C=90°,AB=5,BC=4,∴sinA==,故选D.2.抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为()A.B.C.D.21世纪教育网www.21cnjy.com精品资料·第1页(共14页)版权所有@21世纪教育网登陆21世纪教育助您教考全无忧3.若一个三角形三个内角度数的比为1:2:3,那么这个三角形最小角的正切值为()A.B.C.D.解: 三角形三个内角度数的比为1:2:3,∴设三个内角分别为k、2k、3k,∴k+2k+3k=180°,解得k=30°,最小角的正切值=tan30°=.故选:C.4.关于抛物线y=﹣(x+2)2+1,下列说法正确的是()A.当x=2时,y有最小值1B.当x=2﹣时,y有最大值1C.当x=2时,y有最大值1D.当x=2﹣时,y有最小值1解:抛物线y=﹣(x+2)2+1当x=2﹣时有最大值1,故选B.5.如图,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为()21世纪教育网www.21cnjy.com精品资料·第2页(共14页)版权所有@21世纪教育网登陆21世纪教育助您教考全无忧A.cm2B.cm2C.cm2D.cm2解:如图,由题可知△ABC是一个顶角为45°的等腰三角形,即∠A=45°,AC=AB.作CD⊥AB,垂足为D,则CD=1. sin∠A=,∴==AB,∴S△ABC=×AB×CD=,∴折叠后重叠部分的面积为cm2.故选D.6.如图,△ABC是锐角三角形,sinC=,则sinA的取值范围是()A.0B.C.D.解:作AH⊥BC于H,如图,在Rt△ACH中,sinC==,设AH=4x,AC=5x,所以CH==3x,所以sin∠HAC==, ∠HAC<∠BAC<90°,∴<sin∠BAC<1.故选D.21世纪教育网www.21cnjy.com精品资料·第3页(共14页)版权所有@21世纪教育网登陆21世纪教育助您教考全无忧7.已知二次函数y=(k2﹣)x2+2x+1的图象与x轴有交点,则k的取值范围是()A.k≥3B.k<3C.k≤3且k≠2D.k<2解: 二次函数y=(k2﹣)x2+2x+1的图象与x轴有交点,∴一元二次方程(k2﹣)x2+2x+1=0有解,∴,解得:k≤3且k≠2.故选:C.8.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要()A.米2B.米2C.(4+)米2D.(4+4tanθ)米2解:在R...