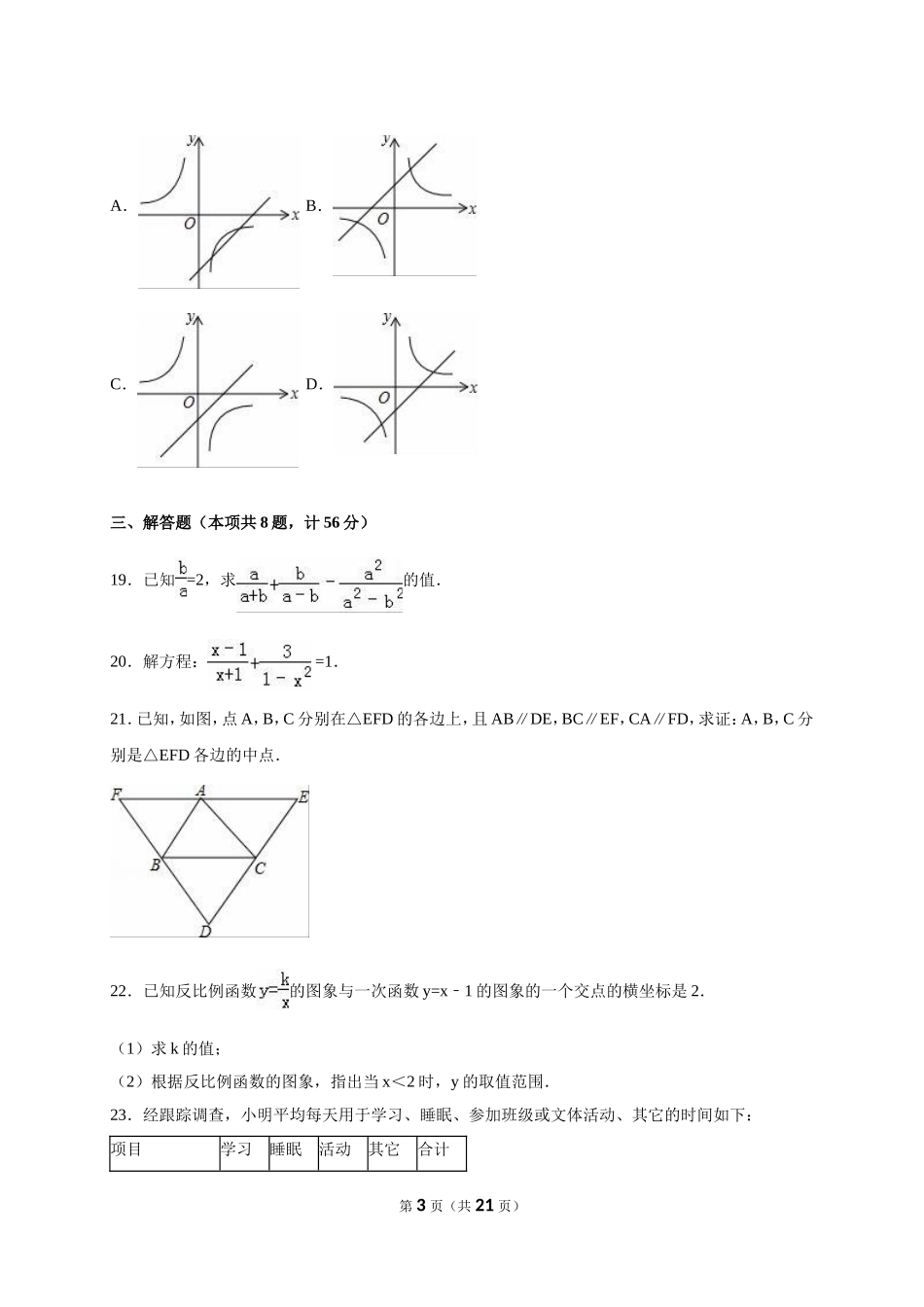
2017-2018学年江苏省盐城市东台市八年级(下)期末数学试卷一、填空题(本项共10题,每题2分,计20分)1.当x等于时,分式无意义.2.国际奥委会于2001年7月13日通过投票确定2008年奥运会举办城市,北京获得总计105张选票中的56张,得票率超过50%,获得奥运会举办权.北京得票的频数是.3.小明某周每天的睡眠时间是(单位:h):8,9,7,9,8,8,7.这组数据的众数是.4.反比例函数的图象在第二、四象限,则k的取值范围是.5.计算:2+﹣=.6.下表是某批足球质量检验获得的数据,请根据此表回答,当抽取的足球数很大时,这批足球优等品的频率会在常数附近摆动.抽取的足球数5010020050010002000优等品数479519447295319027.方程x23x=0﹣的解是.8.菱形的边长为5,一条对角线长为8,则其面积为.9.已知:,则m=.10.如图,将边长为的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=.第1页(共21页)二、选择题(本项共8题,每题3分,计24分)11.下列调查适合用普查的是()A.长江中现有鱼的种类B.某品牌灯泡的使用寿命C.全校学生最喜爱的体育项目D.一批食品中防腐剂的含量12.下列计算正确的是()A.B.C.D.13.某商店6月份的利润是25000元,要使8月份的利润至少达到36000元,则平均每月利润增长的百分率不低于()A.10%B.20%C.44%D.120%14.正方形具有而菱形不一定具有的性质是()A.对角线互相平分B.对角线相等C.对角线互相垂直D.对角线平分对角15.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是()A.=B.=C.=D.=16.一组数据:2,3,2x,4,2,x+1的中位数是3,则x的值是()A.1B.2C.3D.17.在矩形ABCD中,点E在CD上,且BE平分∠AEC,若∠DAE=30°,BE=2,则AD=()A.B.2C.1D.18.在平面直角坐标系中,函数y=与y=x+k的图象不可能是下列图形中的()第2页(共21页)A.B.C.D.三、解答题(本项共8题,计56分)19.已知=2,求的值.20.解方程:=1.21.已知,如图,点A,B,C分别在△EFD的各边上,且AB∥DE,BC∥EF,CA∥FD,求证:A,B,C分别是△EFD各边的中点.22.已知反比例函数的图象与一次函数y=x1﹣的图象的一个交点的横坐标是2.(1)求k的值;(2)根据反比例函数的图象,指出当x<2时,y的取值范围.23.经跟踪调查,小明平均每天用...