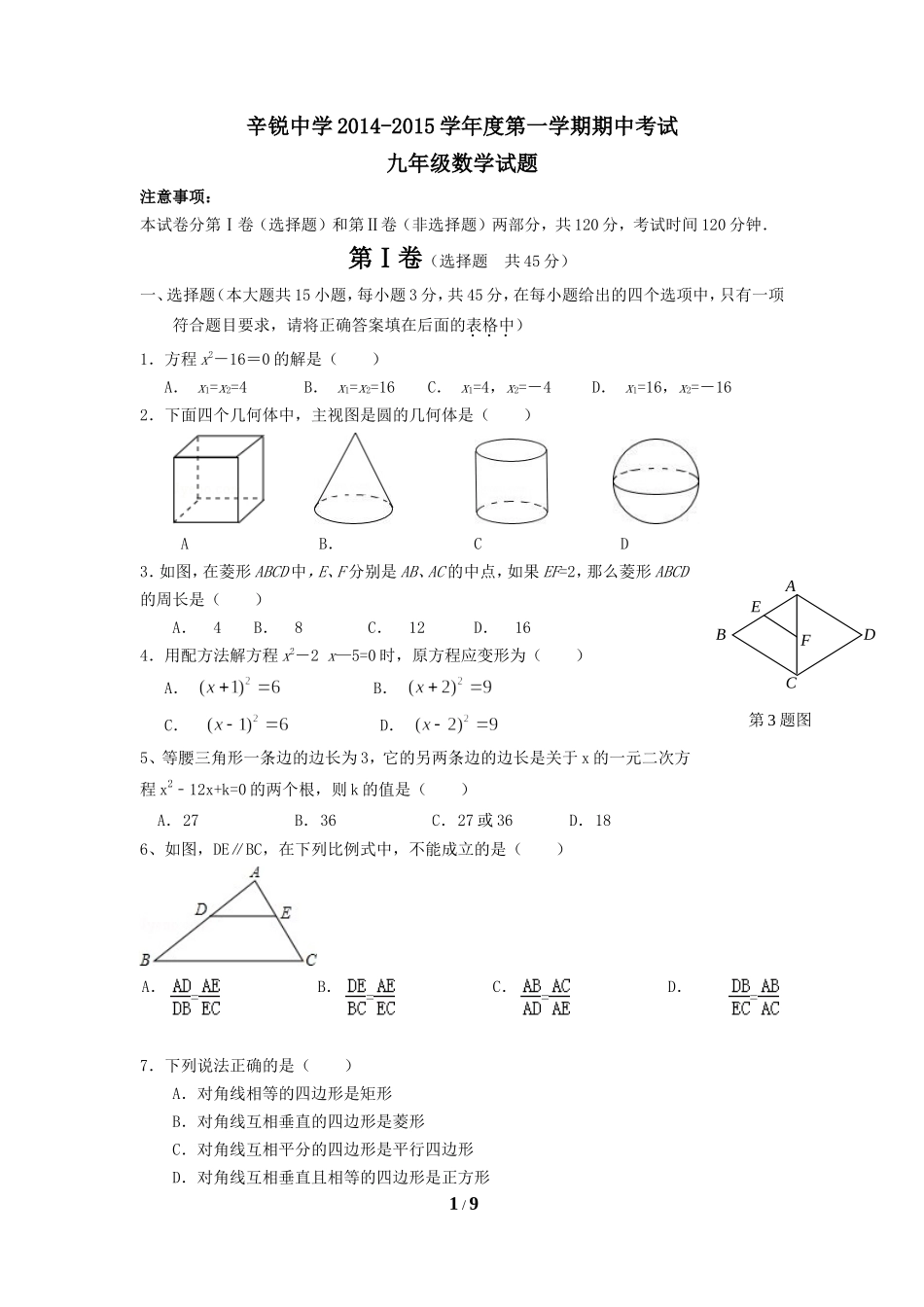
辛锐中学2014-2015学年度第一学期期中考试九年级数学试题注意事项:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分,考试时间120分钟.第Ⅰ卷(选择题共45分)一、选择题(本大题共15小题,每小题3分,共45分,在每小题给出的四个选项中,只有一项符合题目要求,请将正确答案填在后面的表格中)1.方程x2-16=0的解是()A.x1=x2=4B.x1=x2=16C.x1=4,x2=-4D.x1=16,x2=-162.下面四个几何体中,主视图是圆的几何体是()AB.CD3.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是()A.4B.8C.12D.164.用配方法解方程x2-2x—5=0时,原方程应变形为()A.B.C.D.5、等腰三角形一条边的边长为3,它的另两条边的边长是关于x的一元二次方程x2﹣12x+k=0的两个根,则k的值是()A.27B.36C.27或36D.186、如图,DE∥BC,在下列比例式中,不能成立的是()A.=B.=C.=D.=7.下列说法正确的是()A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直且相等的四边形是正方形1/9EABCDF第3题图8.某药品经过两次降价,每瓶零售价由168元降为128元,已知两次降价的百分率相同,每次降价的百分率为x,根据题意列方程得()A.168(1+x)2=128B.168(1-x)2=128C.128(1-x)2=168D.128(1-x)2=1689、如图所示,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=,AC=3,则CD的长为()A.1B.4C.3D.[来源:学*科*网]210.如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC交AB于D,E为垂足,连接CD,若BD=1,则AC的长是()A.2B.2C.4D.411.若关于的一元二次方程有两个不相等的实数根,则的取值范围是()A.B.且C.D.且12.有三张正面分别写有数字﹣1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为()A.B.C.D.13.平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()A.AB=BCB.AC=BDC.AC⊥BDD.AB⊥BD14已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=().A.B.C.D.215、如图,正方形ABCD的面积为1,M是AB的中点,则图中阴影部分的面...