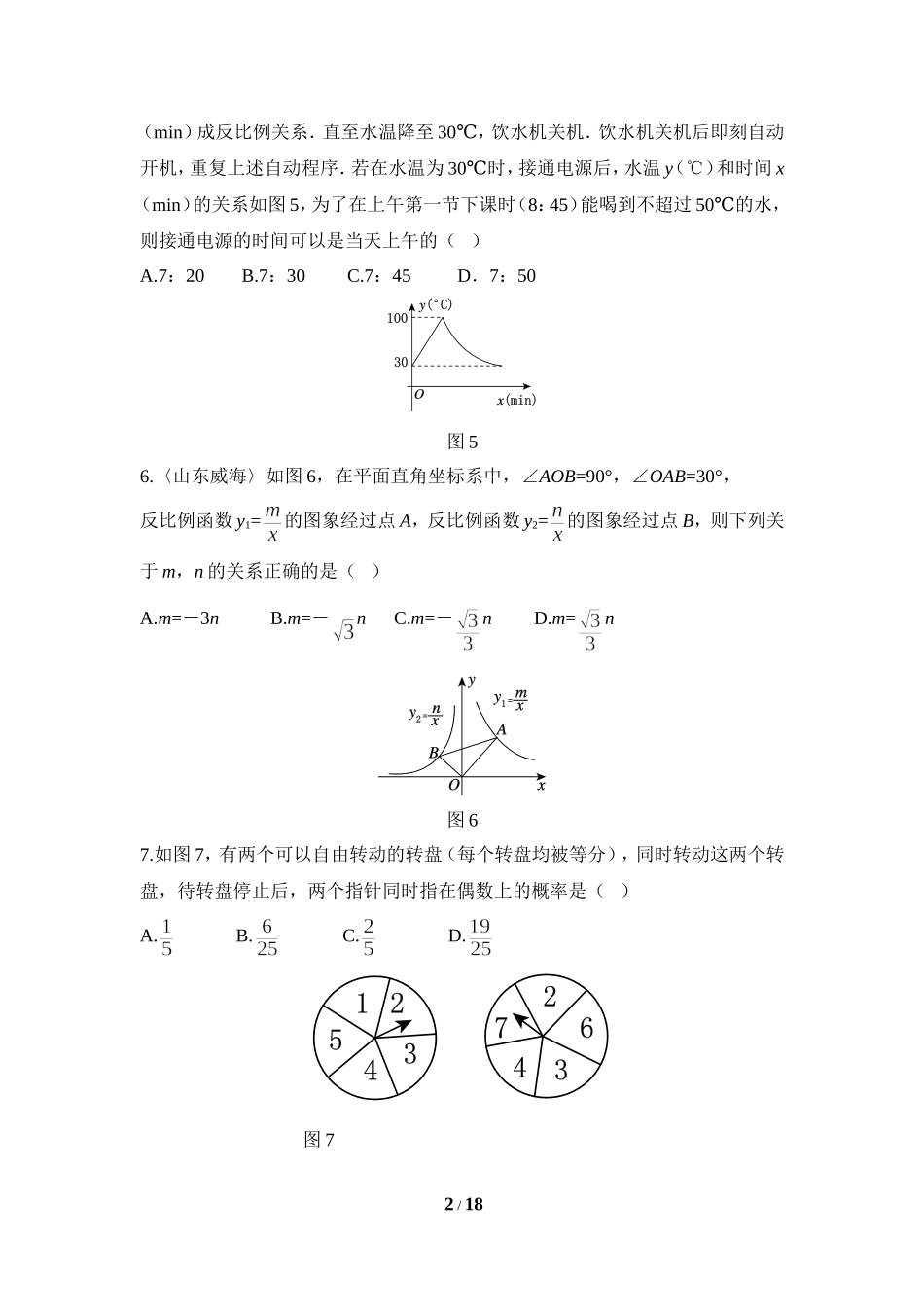
期末选优拔尖测试卷(120分,120分钟)一、选择题(每题3分,共36分)1.已知x-=3,则4-x2+x的值为()A.1B.C.D.2.(吉林长春)如图1,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=x上,则点B与其对应点B′间的距离为()A.B.3C.4D.5图13.如图2的几何体的左视图是图3中的()图2图3图44.〈山东临沂〉如图4,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2),分别以A1,A2,B1,B2其中的任意两点与点O为顶点作三角形,所作三角形是等腰三角形的概率是()A.B.C.D.5.〈浙江绍兴〉教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时x1/18(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图5,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的()A.7:20B.7:30C.7:45D.7:50图56.〈山东威海〉如图6,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=的图象经过点A,反比例函数y2=的图象经过点B,则下列关于m,n的关系正确的是()A.m=-3nB.m=-nC.m=-nD.m=n图67.如图7,有两个可以自由转动的转盘(每个转盘均被等分),同时转动这两个转盘,待转盘停止后,两个指针同时指在偶数上的概率是()A.B.C.D.图72/188.〈山东滨州〉如图8,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:①AD=BC;②BD,AC互相平分;③四边形ACED是菱形.其中正确的个数是()A.0B.1C.2D.3图8图99.如图9是某几何体的三视图,则组成该几何体的小方块块数为()A.12块B.9块C.7块D.6块10.〈青海西宁〉已知函数y=kx+b的图象如图10所示,则一元二次方程x2+x+k-1=0根的存在情况是()A.没有实数根B.有两个相等的实数根C.有两个不相等的实数根D.无法确定图10图1111.〈山东菏泽,有改动〉如图11,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16B.17C.18D.1912.根据如图12所示的程序,得到了y与x的函数图象(如图13),过y轴正半轴上一点M作PQ∥x轴交图象于点P,Q,连接OP,OQ,则以下结论:①x<0时,y=;②△OPQ的...