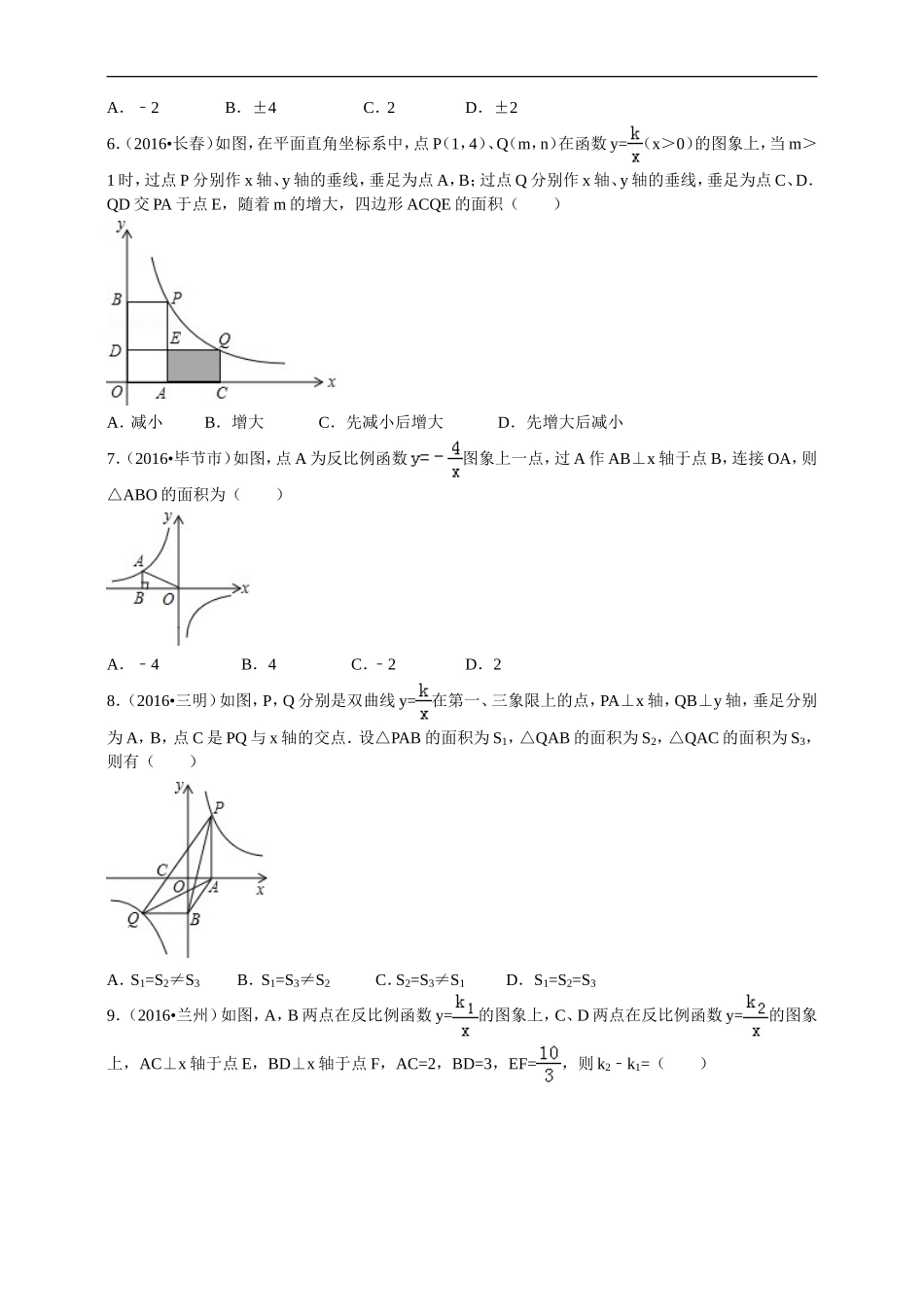
2017--2018学年度第一学期北师版数学九年级单元检测题第六章《反比例函数》B一.选择题(共12小题)1.函数y=(m2m﹣)是反比例函数,则()A.m≠0B.m≠0且m≠1C.m=2D.m=1或22.定义:[a,b]为反比例函数(ab≠0,a,b为实数)的“关联数”.反比例函数的“关联数”为[m,m+2],反比例函数的“关联数”为[m+1,m+3],若m>0,则()A.k1=k2B.k1>k2C.k1<k2D.无法比较3.(2016•锦州)在同一直角坐标系中,一次函数y=axa﹣与反比例函数y=的图象可能是()A.B.C.D.4.如图,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=与y=﹣的图象均与正方形ABCD的边相交,则图中阴影部分的面积之和是()A.2B.4C.6D.85.如图,点A、点B是函数y=的图象上关于坐标原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积是4,则k的值是()A.﹣2B.±4C.2D.±26.(2016•长春)如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积()A.减小B.增大C.先减小后增大D.先增大后减小7.(2016•毕节市)如图,点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为()A.﹣4B.4C.﹣2D.28.(2016•三明)如图,P,Q分别是双曲线y=在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC的面积为S3,则有()A.S1=S2≠S3B.S1=S3≠S2C.S2=S3≠S1D.S1=S2=S39.(2016•兰州)如图,A,B两点在反比例函数y=的图象上,C、D两点在反比例函数y=的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=,则k2k﹣1=()A.4B.C.D.610.(2016•株洲)已知,如图一次函数y1=ax+b与反比例函数y2=的图象如图示,当y1<y2时,x的取值范围是()2·1·c·n·j·yA.x<2B.x>5C.2<x<5D.0<x<2或x>511.(2016•临沂)如图,直线y=x﹣+5与双曲线y=(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是.若将直线y=x﹣+5向下平移1个单位,则所得直线与双曲线y=(x>0)的交点有()A.0个B.1个C.2个D.0个,或1个,或2个12.农大毕业的小王回乡自主创业,在大棚中栽培新品种的蘑菇,该种蘑菇在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培...