2018北师大九年级上第6章反比例函数单元达标检测卷含答案.doc

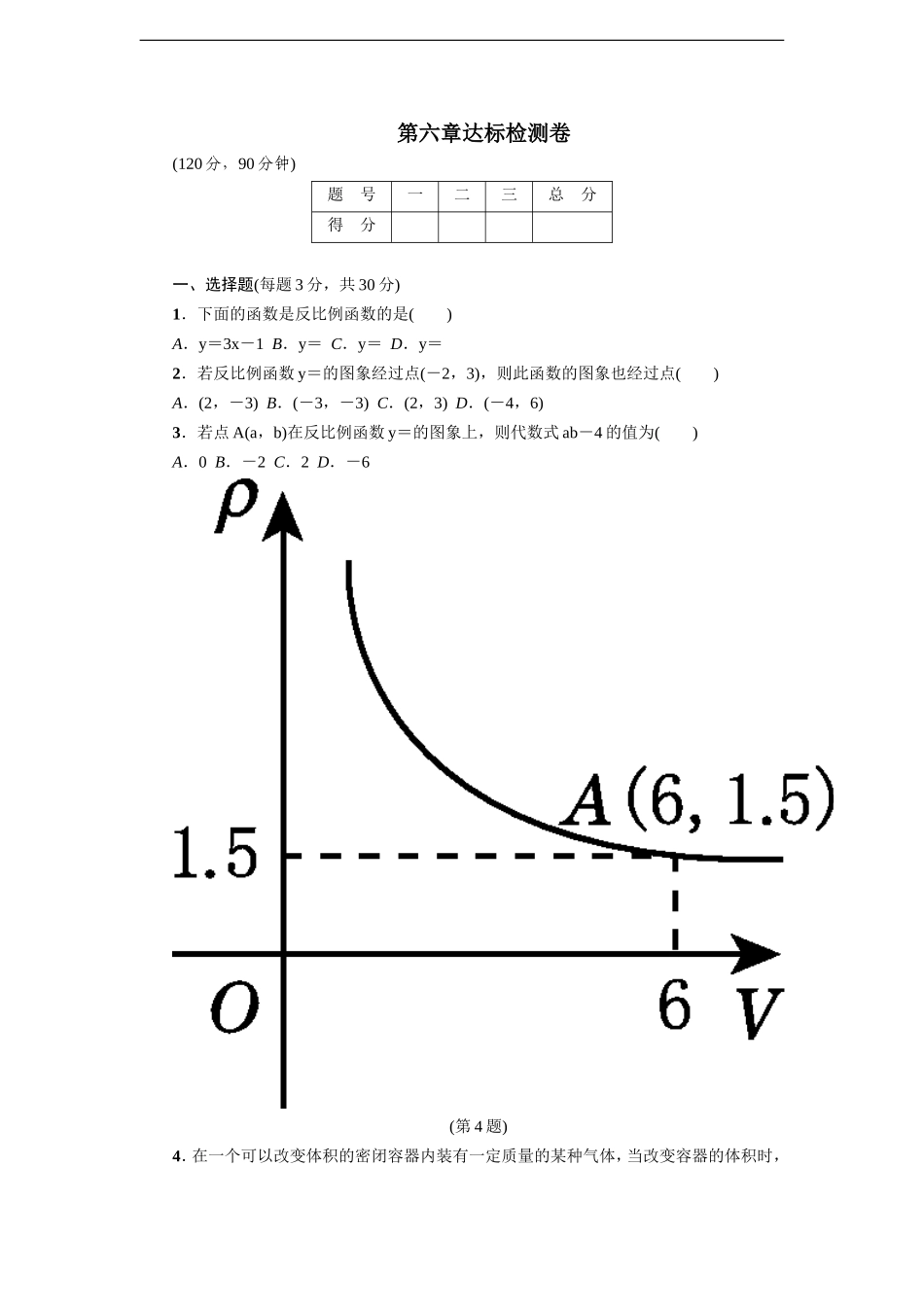
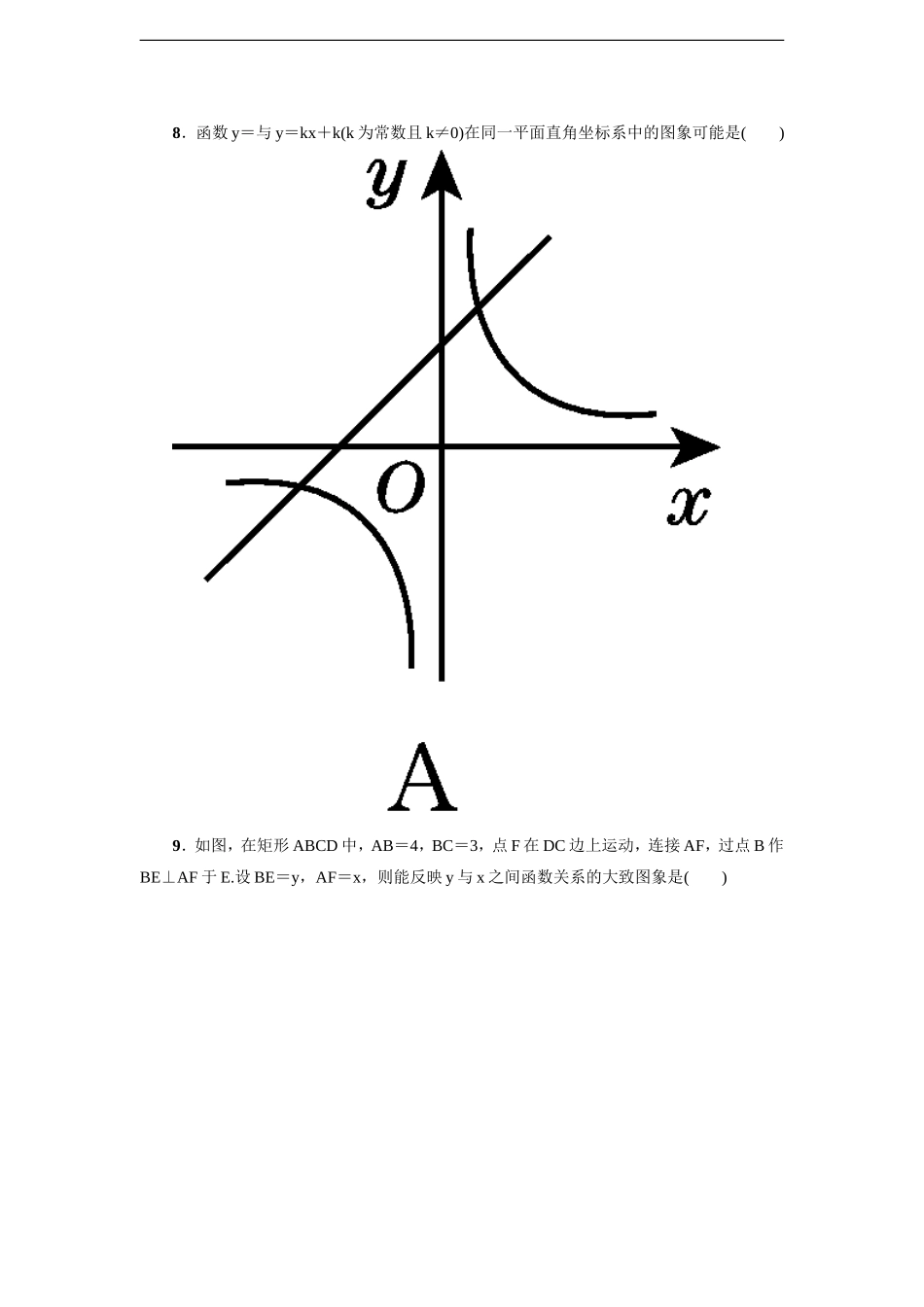
第六章达标检测卷 (120分，90分钟) 题　号 一 二 三 总　分 得　分 一、选择题(每题3分，共30分) 1．下面的函数是反比例函数的是(　　) A．y＝3x－1 B．y＝ C．y＝ D．y＝ 2．若反比例函数y＝的图象经过点(－2，3)，则此函数的图象也经过点(　　) A．(2，－3) B．(－3，－3) C．(2，3) D．(－4，6) 3．若点A(a，b)在反比例函数y＝的图象上，则代数式ab－4的值为(　　) A．0 B．－2 C．2 D．－6 (第4题) 4．在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也会随之改变，密度ρ(单位：kg/m3)与体积V(单位：m3)满足函数关系式ρ＝(k为常数，k≠0)，其图象如图所示，则当气体的密度为3 kg/m3时，容器的体积为(　　) A．9 m3 B．6 m3 C．3 m3 D．1.5 m3 5．若在同一直角坐标系中，正比例函数y＝k1x与反比例函数y＝的图象无交点，则有(　　) A．k1＋k2＞0 B．k1＋k2＜0 C．k1k2＞0 D．k1k2＜0 6．已知点A(－1，y1)，B(2，y2)都在双曲线y＝上，且y1>y2，则m的取值范围是(　　)21教育网 A．m<0 B．m>0 C．m>－3 D．m<－3 (第7题) 7．如图，在直角坐标系中，直线y＝6－x与函数y＝(x＞0)的图象相交于点A，B，设点A的坐标为(x1，y1)，那么长为y1、宽为x1的矩形的面积和周长分别为(　　) A．4，12 B．8，12 C．4，6 D．8，6 8．函数y＝与y＝kx＋k(k为常数且k≠0)在同一平面直角坐标系中的图象可能是(　　) 9．如图，在矩形ABCD中，AB＝4，BC＝3，点F在DC边上运动，连接AF，过点B作BE⊥AF于E.设BE＝y，AF＝x，则能反映y与x之间函数关系的大致图象是(　　) (第9题) 　　 (第10题) 10．如图，△AOB是直角三角形，∠AOB＝90°，OB＝2OA，点A在反比例函数y＝的图象上，若点B在反比例函数y＝的图象上，则k的值是(　　)21·cn·jy·com A．－4 B．4 C．－2 D．2 二、填空题(每题3分，共24分) 11．一个反比例函数的图象过点A(－2，－3)，则这个反比例函数的表达式是________． 12．南宁市五象新区有长24 000 m的新道路要铺上沥青，则铺路所需时间t(天)与铺路速度v(m/天)的函数关系式是________．www.21-cn- 13．点(2，y1)，(3，y2)在函数y＝－的图象上，则y1________y2(填“>”“<”或“＝”)． 14．若反比例函数y＝的图象与一次函数y＝mx的图象的一个交点的坐标为(1，2)，则它们另一个交点的坐标为________．【来源：21·世纪·教育·网】 15．如图，点A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，且△ABP的面积为6，则这个反比例函数的表达式为________．21·世纪*教育网 (第15题) 　　　(第16题) 　　　(第17题) 　　　(第18题) 16．如图，矩形ABCD在第一象限，AB在x轴的正半轴上(点A与点O重合)，AB＝3，BC＝1，连接AC，BD，交点为M.将矩形ABCD沿x轴向右平移，当平移距离为________时，点M在反比例函数y＝的图象上．www-2-1-cnjy-com 17．如图，过原点O的直线与反比例函数y1，y2的图象在第一象限内分别交于点A，B，且A为OB的中点，若函数y1＝，则y2与x的函数表达式是____________． 18．如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A，C分别在x轴，y轴上，反比例函数的图象与正方形的两边AB，BC分别交于点M，N，ND⊥x轴，垂足为D，连接OM，ON，MN.下列结论：①△OCN≌△OAM；②ON＝MN；③四边形DAMN与△MON面积相等；④若∠MON＝45°，MN＝2，则点C的坐标为(0，＋1)．其中正确结论的序号是____________．21*cnjy*com 三、解答题(19～21题每题8分，22～24题每题10分，25题12分，共66分) 19．在平面直角坐标系中，直线y＝x向上平移1个单位长度得到直线l，直线l与反比例函数y＝的图象的一个交点为(a，2)，求k的值．【来源：21cnj*y.co*m】 20．已知反比例函数y＝，当x＝－时，y＝－6. (1)这个函数的图象位于哪些象限？y随x的增大如何变化？ (2)当＜x＜4时，求y的取值范围． 21．已知点A(－2，0)和B(2，0)，点P在函数y＝－的图象上，如果△PAB的面积是6，求点P的坐标． 22．如图，一次函数y＝kx＋5(k为常数，且k≠0)的图象与反比例函数y＝－的图象交于A(－2，b)，B两点．2·1·c·n·j·y (第22题) (1)求一次函数的表达式； (2)若将直线AB向下平移m(m＞0)个单位长度后，与反比例函数的图象有且只有一个公共点，求m的值．【出处：21教育名师】 23．如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A，C分别在y轴，x轴上，点B的坐标为(4，2)，直线y＝－x＋3交AB，BC分别于点M，N，反比例函数y＝的图象经过点M，N.21教育名师原创作品 (1)求反比例函数的表达式； (2)若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标． (第23题) 24．教师办公室有一种可以自动加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10 ℃，待加热到100 ℃，饮水机自动停止加热，水温开始下降，水温y(℃)和通电时间x(min)成反比例函数关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20 ℃，接通电源后，水温y(℃)和通电时间x(min)之间的关系如图所示，回答下列问题： (1)分别求出当0≤x≤8和8＜x≤a时，y和x之间的函数关系式； (2)求出图中a的值； (3)李老师这天早上7：30将饮水机电源打开，若他想在8：10上课前喝到不低于40 ℃的开水，则他需要在什么时间段内接水？ (第24题) 25．如图，正比例函数y＝2x的图象与反比例函数y＝的图象交于A，B两点，过点A作AC垂直x轴于点C，连接BC，若△ABC的面积为2.21*cnjy*com (1)求k的值． (2)x轴上是否存在一点D，使△ABD为直角三角形？若存在，求出点D的坐标；若不存在，请说明理由． (第25题) 答案 一、1.C　2.A　 3．B　点拨：∵点A(a，b)在反比例函数y＝的图象上， ∴ab＝2.∴ab－4＝2－4＝－2. 4．C 5．D　点拨：若k1，k2同正或同负其图象均有交点． 6．D　点拨：由题意知，反比例函数图象在第二、四象限，所以3＋m<0，即m<－3. 7．A　点拨：由反比例函数y＝(k≠0)中的比例系数k的几何意义知矩形的面积为|k|，即为4；因为A(x1，y1)在第一象限，即x1＞0，y1＞0，由直线y＝6－x得x1＋y1＝6，所以矩形的周长为2(x1＋y1)＝12.2-1-c-n-j-y 8．A 9．C　点拨：连接BF，则可知S△AFB＝xy＝×4×3，故y＝，其自变量的取值范围是3≤x≤5，对应的函数值的范围为≤y≤4，故选C. 10．A　点拨：分别过点A，B作AC⊥x轴，BD⊥x轴，垂足分别为点C，D.易知∠AOC＋∠BOD＝90°，∠BOD＋∠OBD＝90°，∴∠OBD＝∠AOC.又∠BDO＝∠OCA＝90°.∴△ODB∽△ACO.∴＝＝＝2.设点A的坐标是(m，n)，∵点A在反比例函数y＝的图象上，∴mn＝1. 易知AC＝n，OC＝m，∴BD＝2m，OD＝2n.∴B点的坐标是(－2n，2m)．∵点B在反比例函数y＝的图象上，∴2m＝，即k＝－4mn＝－4. 二、11.y＝ 12．t＝(v>0) 13．< 14．(－1，－2)　点拨：因为反比例函数y＝的图象关于原点成中心对称，一次函数y＝mx的图象经过原点，且关于原点成中心对称，所以它们的交点也关于原点成中心对称．又点(1，2)关于原点成中心对称的点为(－1，－2)，所以它们另一个交点的坐标为(－1，－2)． 15．y＝　点拨：连接OA，则△ABP与△ABO的面积都等于6，所以反比例函数的表达式是y＝. 16.　点拨：将矩形ABCD沿x轴向右平移后，过点M作ME⊥AB于点E，则AE＝AB＝，ME＝BC＝.设OA＝m，则OE＝OA＋AE＝m＋，∴M.∵点M在反比例函数y＝的图象上，【版权所有：21教育】 ∴＝，解得m＝. 17．y2＝ 18．①③④ 三、19.解：∵直线y＝x向上平移1个单位长度得到直线l， ∴直线l对应的函数表达式是y＝x＋1. ∵直线l与反比例函数y＝的图象的一个交点为(a，2)， ∴2＝a＋1.∴a＝1. ∴这个交点坐标是(1，2)． 把点(1，2)的坐标代入y＝， 得2＝，∴k＝3. 20．解：(1)把x＝－，y＝－6代入y＝中，得－6＝， 则k＝2，即反比例函数的表达式为y＝. 因为k＞0，所以这个函数的图象位于第一、第三象限，在每个象限内，y随x的增大而减小． (2)将x＝代入表达式中得y＝4，将x＝4代入表达式中得y＝， 所以y的取值范围为＜y＜4. 21．解：∵点A(－2，0)和B(2，0)， ∴AB＝4. 设点P坐标为(a，b)，则点P到x轴的距离是|b|，又△PAB的面积是6，∴×4|b|＝6. ∴|b|＝3.∴b＝±3. 当b＝3时，a＝－； 当b＝－3时，a＝. ∴点P的坐标为或.　 22．解：(1)根据题意，把A(－2，b)的坐标分别代入一次函数和反比例函数表达式，得 解得所以一次函数的表达式为y＝x＋5. (2)将直线AB向下平移m(m＞0)个单位长度后，直线AB对应的函数表达式为y＝x＋5－m.由得，x2＋(5－m)x＋8＝0.Δ＝(5－m)2－4××8＝0，解得m＝1或9. 23．解：(1)由题意易得点M的纵坐标为2. 将y＝2代入y＝－x＋3，得x＝2. ∴M(2，2)．把点M的坐标代入y＝，得k＝4， ∴反比例函数的表达式是y＝. (2)由题意得S△OPM＝OP·AM， ∵S四边形BMON＝S矩形OABC－S△AOM－S△CON＝4×2－2－2＝4， S△OPM＝S四边形BMON， ∴OP·AM＝4. 又易知AM＝2，∴OP＝4. ∴点P的坐标是(0，4)或(0，－4)． 24．解：(1)当0≤x≤8时，设y＝k1x＋b， 将(0，20)，(8，100)的坐标分别代入y＝k1x＋b，可求得k1＝10，b＝20. ∴当0≤x≤8时，y＝10x＋20. 当8＜x≤a时，设y＝， 将(8，100)的坐标代入y＝， 得k2＝800. ∴当8<x≤a时，y＝. 综上，当0≤x≤8时，y＝10x＋20； 当8＜x≤a时，y＝. (2)将y＝20代入y＝， 解得x＝40，即a＝40. (3)当y＝40时，x＝＝20. ∴要想喝到不低于40 ℃的开水，x需满足8≤x≤20，即李老师要在7：38到7：50之间接水． 25．解：(1)∵正比例函数图象与反比例函数图象的两个交点关于原点对称， ∴S△AOC＝S△BOC＝S△ABC＝1. 又∵AC垂直于x轴，∴k＝2. (2)假设存在这样的点D，设点D的坐标为(m，0)． 由解得 ∴A(1，2)，B(－1，－2)． ∴AD＝， BD＝， AB＝＝2. 当D为直角顶点时， ∵AB＝2，∴OD＝AB＝. ∴D的坐标为(，0)或(－，0)． 当A为直角顶点时， 由AB2＋AD2＝BD2，得(2)2＋(1－m)2＋22＝(m＋1)2＋22， 解得m＝5，即D(5，0)． 当B为直角顶点时， 由BD2＋AB2＝AD2，得(m＋1)2＋22＋(2)2＝(1－m)2＋22， 解得m＝－5，即D(－5，0)． ∴存在这样的点D，使△ABD为直角三角形，点D的坐标为(，0)或(－，0)或(5，0)或(－5，0)．21世纪教育网版权所有