甘肃省会宁县2017-2018一学期期中考试九年级数学试卷.doc

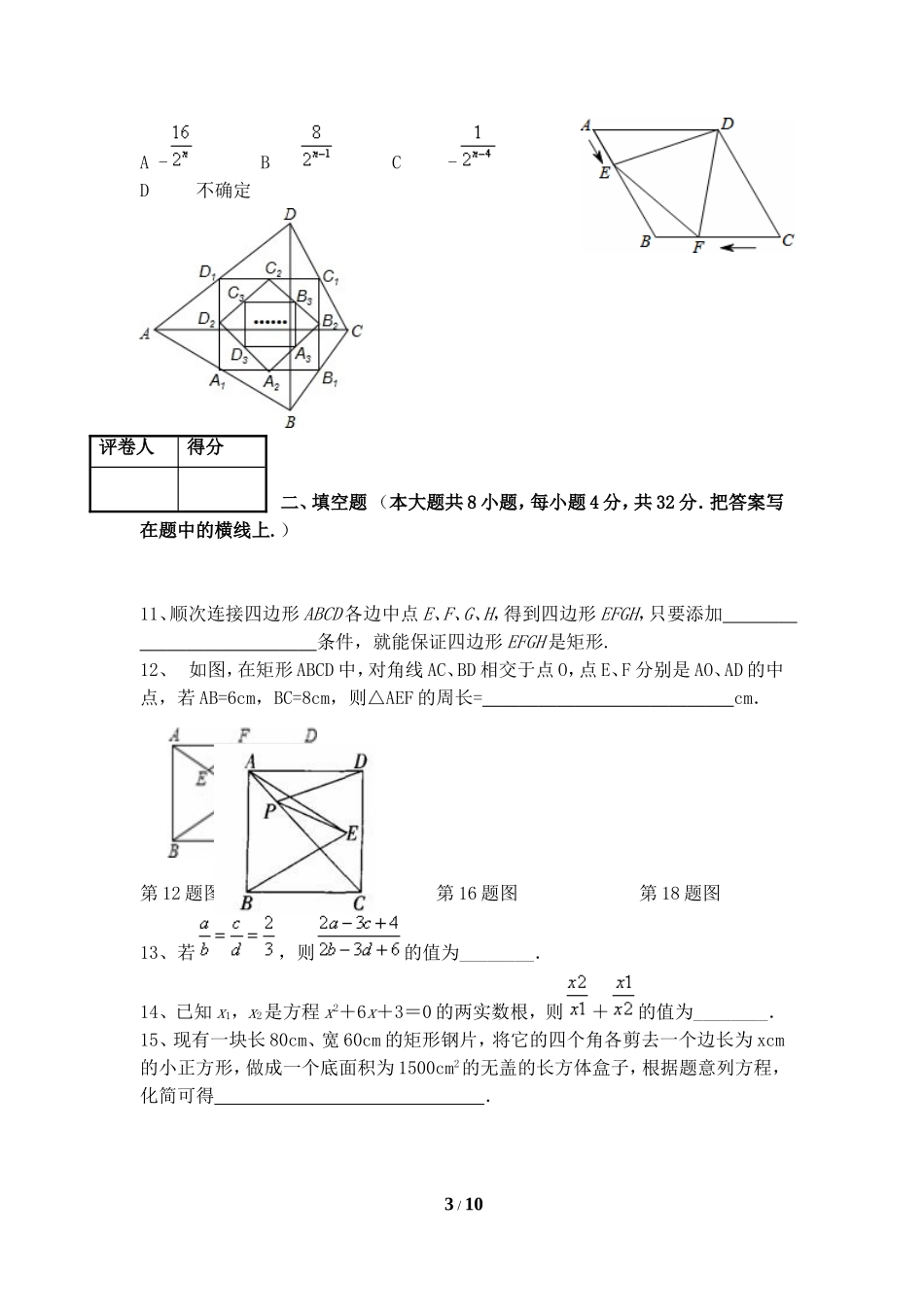
会宁县2017—2018学年度第一学期期中考试 九 年 级 数 学 试 卷 本试卷满分150分，考试时间120分钟 题号 一、选择题 二、填空题 三、计算题（一） 四、计算题（二） 总分 得分 评卷人 得分 一、选择题（本大题共10个小题，每小题3分，共30分，每小题给出的四个选项中，只有一项是符合题目要求的，将此选项的字母填填在括号中)． 1、下列命题中正确的是（　　） A． 有一组邻边相等的四边形是菱形 B． 有一个角是直角的平行四边形是矩形 C． 对角线垂直的平行四边形是正方形 D． 一组对边平行的四边形是平行四边形 2、下面关于的方程中：①；②；③；④（）；⑤=-1.一元二次方程的个数是（   ） A.1      B.2     C.3       D.4 3、如图，菱形ABCD中，AB=4，∠B=60°，AE⊥BC，AF⊥CD，垂足分别为E，F，连接EF，则的△AEF的面积是（　　） A 4 B 3 C 2 D 4、在一个口袋中有4个完全相同的小球，它们的标号分别为1，2，3，4，从中随机摸出一个小球记下标号后放回，再从中随机摸出一个小球，则两次摸出的小球的标号之和大于4的概率是（　　） A．    B．       C．        D． 5、如图，在矩形ABCD中，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点，当点P在BC上从B向C移动而R不动时，那么下列结论成立的是（     ） （A）线段EF的长逐渐增大  （B）线段EF的长逐渐减少 （C）线段EF的长不变    （D）线段EF的长不能确定 6、如图，AB∥CD∥EF，则在图中下列关系式一定成立的是（　　） A．    B．      C．     D． 7、 根据下列表格对应值： 3.24 3.25 3.26 -0.02 0.01 0.03 判断关于的方程的一个解的范围是（   ） A. ＜3.24    B. 3.24＜＜3.25 C.3.25＜＜3.26   D. 3.25＜＜3.28 8、若关于x 的一元二次方程有解，那么m的取值范围是（  ） A.   B.    C. 且  D. 且 9、某市2013年投入教育经费2亿元，为了发展教育事业，该市每年教育经费的年增长率均为x，从2013年到2015年共投入教育经费9.5亿元,则下列方程正确的是（   ） A.  B．  C．  D． 10、如图，四边形ABCD中，对角线AC⊥BD，且AC=8，BD=4，各边中点分别为A1、B1、C1、D1，顺次连接得到四边形A1B1C1D1，再取各边中点A2、B2、C2、D2，顺次连接得到四边形A2B2C2D2，……，依此类推，这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为（    ） A -    B     C   -   D   不确定 评卷人 得分 二、填空题 （本大题共8小题，每小题4分，共32分．把答案写在题中的横线上.） 11、顺次连接四边形ABCD各边中点E、F、G、H，得到四边形EFGH，只要添加              条件，就能保证四边形EFGH是矩形. 12、 如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则△AEF的周长=              cm． 第12题图 第16题图 第18题图 13、若，则的值为________． 14、已知x1，x2是方程x2＋6x＋3＝0的两实数根，则＋的值为________． 15、现有一块长80cm、宽60cm的矩形钢片，将它的四个角各剪去一个边长为xcm的小正方形，做成一个底面积为1500cm2的无盖的长方体盒子，根据题意列方程，化简可得　 　． 16、如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD＋PE的和最小，则这个最小值为        ． 17、在比例尺为1：5 000 000的地图上，量得甲、乙两地的距离约为25厘米，则甲、乙两地的实际距离约为       千米； 18、如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为　 　． 评卷人 得分 三、解答题（一）：本大题共5小题，共38分．解答时，应写出必要的文字说明、证明过程或演算步骤. 19、解下列方程（每小题3分，共12分） （1）　（公式法） （2） 7x2 -23x +6 = 0. （配方法） (3)  （分解因式法）       （4）解方程：（适当的方法） 20、设x、y均为实数，且，求的值．（5分） 21、设a是方程的一个根，求代数式的值．（5分） 22、（6分）如图所示，四边形ABCD∽四边形，求未知边的长度和的度数。 23、（共10分）如图，在Rt△ABC中，∠ACB=90，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE （1）求证：CE=AD （2）当点D在AB中点时，四边形BECD是什么特殊四边形？说明理由 （3）若D为AB的中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？说明理由。 评卷人 得分 四、解答题（二）：本大题共5小题，共50分．解答时，应写出必要的文字说明、证明过程或演算步骤. 24、（共8分）已知：平行四边形ABCD的两边AB、BC的长是关于的方程的两个实数根． （1）试说明：无论取何值方程总有两个实数根 （2）当为何值时，四边形ABCD是菱形？求出这时菱形的边长； （3）若AB的长为2，那么平行四边形ABCD的周长是多少？ 25、(共10分）已知关于x的方程x2－2(k－1)x＋k2＝0有两个实数根x1，x2. (1)求k的取值范围； (2)若|x1＋x2|＝x1x2－1，求k的值． 26、（共10分）小莉的爸爸买了某演唱会的一张门票，她和哥哥两人都很想去观看，可门票只有一张，读九年级的哥哥想了一个办法，拿了八张扑克牌，将数字为1，2，3，5的四张牌给小莉，将数字为4，6，7，8的四张牌留给自己，并按如下游戏规则进行：小莉和哥哥从各自的四张牌中随机抽出一张，然后将抽出的两张牌数字相加，如果和为偶数，则小莉去；如果和为奇数，则哥哥去． （1）请用树状图或列表的方法表示出两张牌数字相加和的所有可能出现的结果； （2）哥哥设计的游戏规则公平吗？为什么？若不公平，请设计一种公平的游戏规则． 27、（共10分）西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售，每天可售出200千克．为了促销，该经营户决定降价销售．经调查发现，这种小型西瓜每降价0.1元/千克，每天可多售出40千克．另外，每天的房租等固定成本共24元．该经营户要想每天盈利200元，应将每千克小型西瓜的售价降低多少元? 28、（共12分）如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（3，3）．将正方形ABCO绕点A顺时针旋转角度α（0°＜α＜90°），得到正方形ADEF，ED交线段OC于点G，ED的延长线交线段BC于点P，连AP、AG． （1）求证：△AOG≌△ADG； （2）求∠PAG的度数；并判断线段OG、PG、BP之间的数量关系，说明理由； （3）当∠1=∠2时，求直线PE的解析式； 【注：】 （4）在（3）的条件下，直线PE上是否存在点M，使以M、A、G为顶点的三角形是等腰三角形，若存在，请直接写出M点坐标；若不存在，请说明理由． 参考答案 一、选择题 1、B． 2、B  3、B  4、C 5、C 6、C 7、B 8、D 9、D 10、B 二、填空题： 11、 12、9 13、2/3 14、10 15、x2﹣70x+825=0 16、 17、1250 18、 三、 计算题（一） 19 （1）、 （2）、3， （3）、 （4）、， 20、  21、-1． 22、由题意得：，∴＝18，∵∠＝360°－（63°＋129°＋78°）＝90°，∵四边形ABCD∽四边形，∴∠C＝∠＝90°，即＝90°． 23、（1）证明：∵DE⊥BC,∠ACB=90°∴AC∥DE,又∵MN∥AB, ∴四边形CADE是平行四边形，∴CE=AD. （2）四边形BECD是菱形，理由：D是AB边的中点，所以AD=DB,又AD=CE,所以DB=CE,而DB∥CE,四边形DBEC是平行四边形，因为ΔACB是直角三角形，D是斜边AB的中点，所以CD=DB,所以四边形BECD是菱形。 （3）∠A=45°时，四边形BECD是正方形，理由：∵∠ACB=90°又∠A=45°∴CA=CB,点D是AB的中点，∴CD⊥AB,即∠CDB=90°，而四边形BECD是菱形，∴四边形BECD是正方形。 四、 计算题（二） 24、（1）  ∵无论m取何值 ∴无论取何值方程总有两个实数根 （2）∵四边形ABCD是菱形 ∴AB=BC即 ∴m=1代入方程得      ∴ ∴ 即菱形的边长为 （3）将AB=2代入方程解得m= 将带入方程 解得（或用根与系数的关系求得） 即BC= ∴周长为5 25、解：(1)由方程有两个实数根，可得 Δ＝b2－4ac＝4(k－1)2－4k2 ＝4k2－8k＋4－4k2＝－8k＋4≥0. 解得k≤. (2)依据题意，可得x1＋x2＝2(k－1)． 由(1)可知k≤， ∴2(k－1)＜0，x1＋x2＜0. ∴|x1＋x2|＝－x1－x2＝x1·x2－1. ∴－2(k－1)＝k2－1. 解得k1＝1(舍去)，k2＝－3. ∴k的值是－3. 26、解：（1） 4 6 7 8 1 1+4=5 1+6=7 1+7=8 1+8=9 2 2+4=6 2+6=8 2+7=9 2+8=10 3 3+4=7 3+6=9 3+7=10 3+8=11 5 5=4=9 5+6=11 5+7=12 5+8=13 由上表可知，两张牌数字相加和的所有可能出现的结果共有16种． （2）不公平．因为上述16种结果出现的可能性相同，而和为偶数的结果有6种，和为奇数的结果有10种，即小莉去的概率为，哥哥去的概率为，，小莉去的概率低于哥哥去的概率．可把小莉的数字5的牌与哥哥数字4的牌对调，使两人去的概率相同，即游戏公平． 27、解：设应将每千克小型西瓜的售价降低元， 根据题意得： 解这个方程得：   答：应将每千克小型西瓜的售价降低0.2或0.3元 28、（1）证明：由题意得， AO=AD，∠AOG=∠ADG=90°， ∴在Rt△AOG和Rt△ADG中，AO=AD，AG=AG， ∴△AOG≌△ADG（HL）. （2）∠PAG =45°,PG=OG+BP.理由如下： 由（1）同理可证△ADP≌△ABP，则∠DAP=∠BAP，DP=BP， ∵由（1）△AOG≌△ADG，∴∠1=∠DAG，DG=OG， 又∵∠1+∠DAG+∠DAP+∠BAP=90°， ∴2∠DAG+2∠DAP=90°，即∠DAG+∠DAP=45°，∴∠PAG=∠DAG+∠DAP=45°. ∴PG=DG+DP=OG+BP. （3）解：∵△AOG≌△ADG，∴∠AGO=∠AGD， 又∵∠1+∠AGO=90°，∠2+∠PGC=90°，∠1=∠2， ∴∠AGO=∠AGD=∠PGC， 又∵∠AGO+∠AGD+∠PGC=180°，∴∠AGO=∠AGD=∠PGC=60°， ∴∠1=∠2=30°， 在Rt△AOG中，AO=3，AG=2OG，AG2=AO2+OG2， ∴OG=，则G点坐标为：（，0）， CG=3﹣，在Rt△PCG中， PG=2CG=2（3﹣），PC==3﹣3，则P点坐标为：（3，3﹣3）， 设直线PE的解析式为y=kx+b， 则，解得， 所以，直线PE的解析式为y=x﹣3． （4）、. 12 / 12