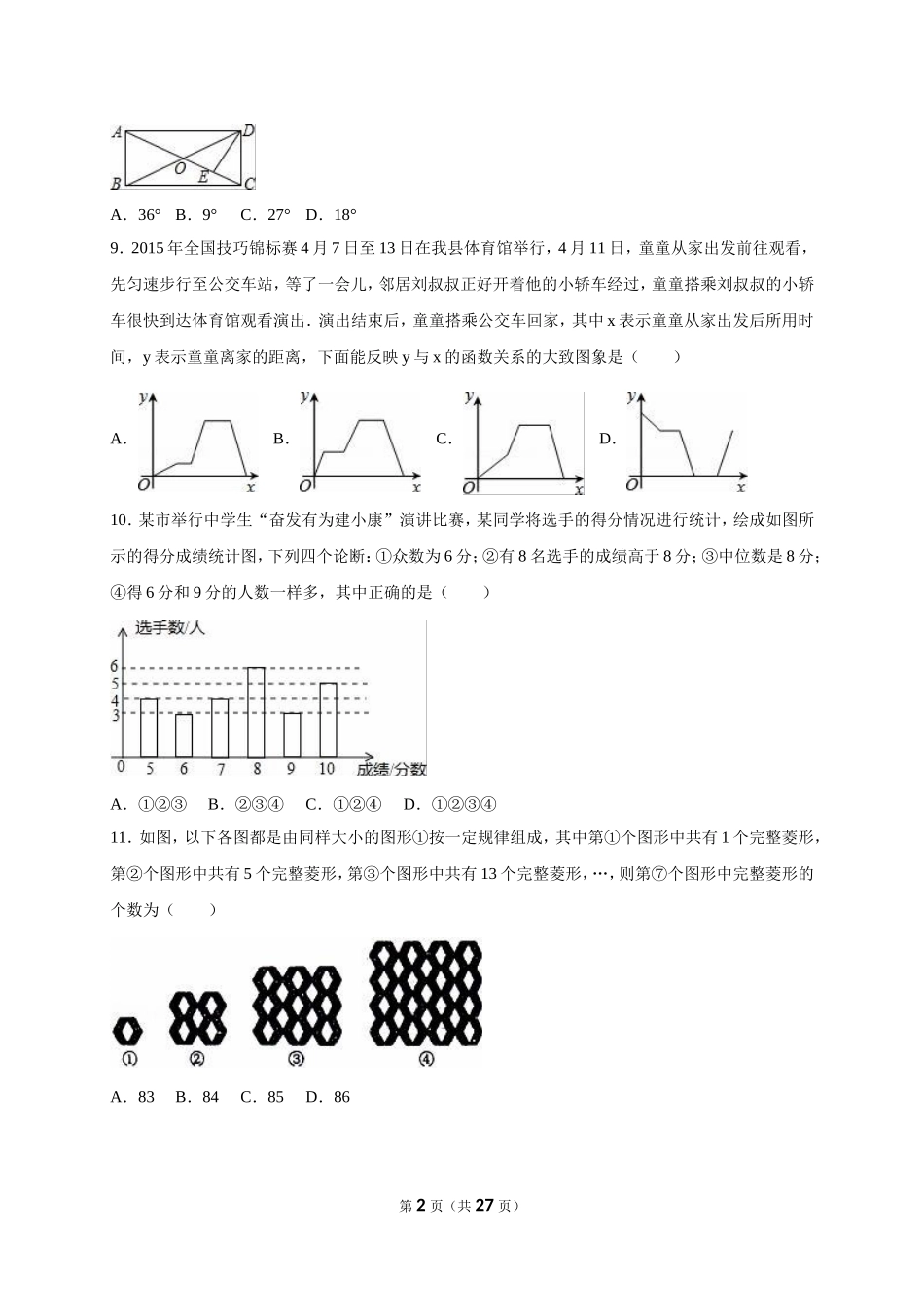
2017-2018学年重庆市垫江县八年级(下)期末数学试卷一、选择题(本大题共12个小题,每小题4分,共48分)四个答案中只有一个是正确的,请将正确答案对应的代号填在答题卷表格各小题对应的空格中。1.下列的式子一定是二次根式的是()A.B.C.D.2.Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为()A.8B.4C.6D.无法计算3.关于四边形ABCD:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等;以上四个条件中可以判定四边形ABCD是平行四边形的有()A.1个B.2个C.3个D.4个4.一次函数y=2x+3﹣的图象不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限5.某校八年级五班有7个合作学习小组,各学习小组的人数分别为:5,5,6,x,7,7,6,已知这组数据的平均数是6,则这组数据的众数和中位数分别是()A.7,6B.6,6C.5,5D.7,76.下列二次根式中属于最简二次根式的是()A.B.C.D.7.如图,一个底面圆周长为24m,高为5m的圆柱体,一只蚂蚁沿侧表面从点A到点B所经过的最短路线长为()A.12mB.15mC.13mD.9.13m8.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为()第1页(共27页)A.36°B.9°C.27°D.18°9.2015年全国技巧锦标赛4月7日至13日在我县体育馆举行,4月11日,童童从家出发前往观看,先匀速步行至公交车站,等了一会儿,邻居刘叔叔正好开着他的小轿车经过,童童搭乘刘叔叔的小轿车很快到达体育馆观看演出.演出结束后,童童搭乘公交车回家,其中x表示童童从家出发后所用时间,y表示童童离家的距离,下面能反映y与x的函数关系的大致图象是()A.B.C.D.10.某市举行中学生“奋发有为建小康”演讲比赛,某同学将选手的得分情况进行统计,绘成如图所示的得分成绩统计图,下列四个论断:①众数为6分;②有8名选手的成绩高于8分;③中位数是8分;④得6分和9分的人数一样多,其中正确的是()A.①②③B.②③④C.①②④D.①②③④11.如图,以下各图都是由同样大小的图形①按一定规律组成,其中第①个图形中共有1个完整菱形,第②个图形中共有5个完整菱形,第③个图形中共有13个完整菱形,…,则第⑦个图形中完整菱形的个数为()A.83B.84C.85D.86第2页(共27页)12.如图,▱ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①AF=CG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°;其中...