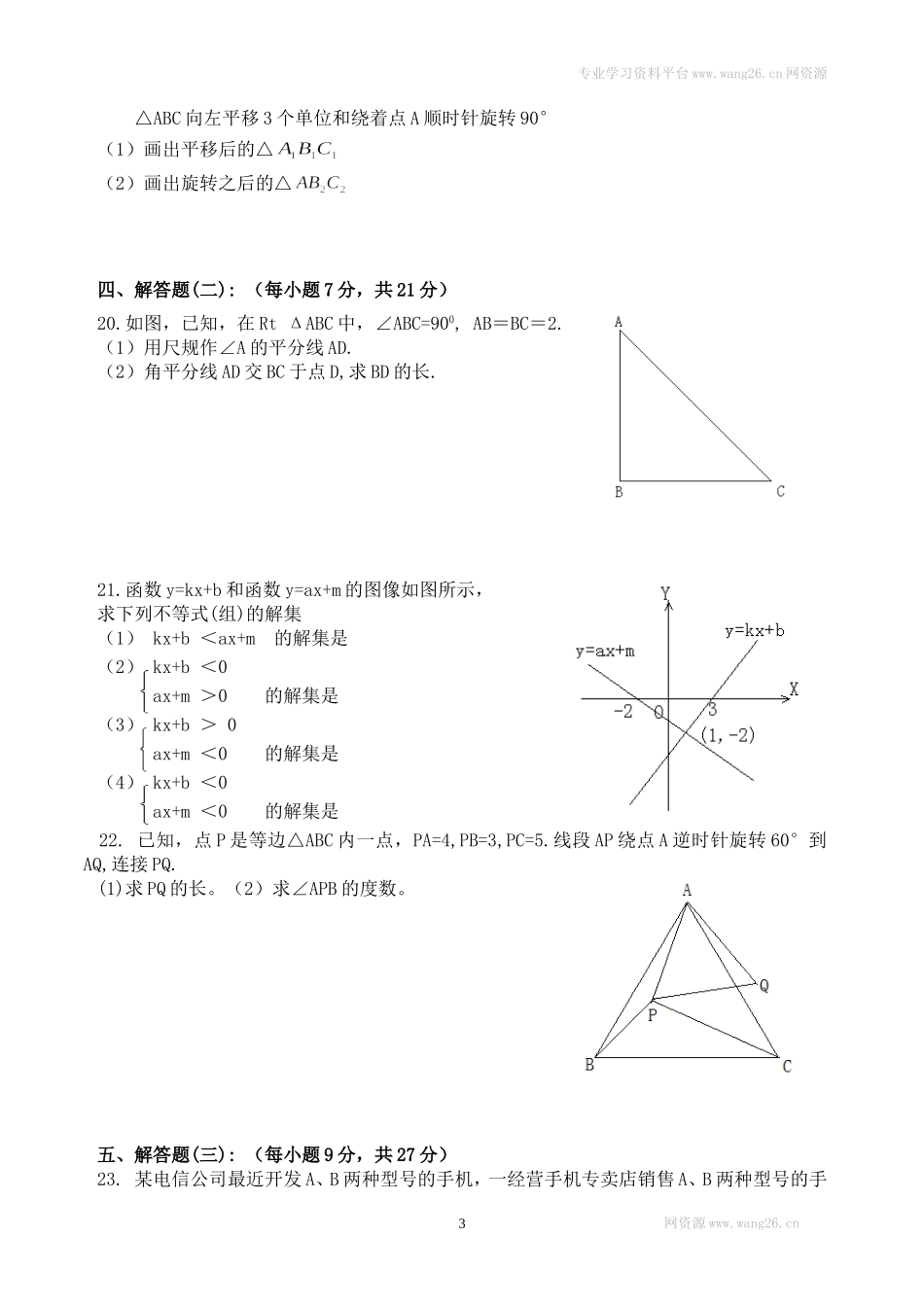
专业学习资料平台www.wang26.cn网资源2017-2018年八年级下第一次月考数学试卷一、选择题(每小题3分,共30分)1.已知等腰三角形的两边长分别为6㎝、3㎝,则该等腰三角形的周长是()A.9㎝B.12㎝C.12㎝或15㎝D.15㎝2.如果,那么下列各式一定正确的是()A.B.C.D.3.下列命题中正确的是()A.有两条边分别相等的两个等腰三角形全等B.两腰对应相等的两个等腰三角形全等C.有两条边分别相等的两个直角三角形全等D.斜边和一条直角边对应相等的两个直角三角形全等4.下列图形中只能用其中一部分平移可以得到的是().ABCD5.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2,则AE的长为()A.B.1C.D.2(第5题图)(第6题图)6.函数y=kx+b(k、b为常数,k0)的图象如图所示,则关于x的不等式kx+b>0的解集为().A.x>0B.x<0C.x<2D.x>27.将不等式组的解集在数轴上表示出来,应是().8.已知关于x的不等式组122baxbax的解集为53x,则ab的值为().A.-2B.21C.-4D.419.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()A.35°B.40°C.50°D.65°10.如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的坐标为()网资源www.wang26.cn1ACBD专业学习资料平台www.wang26.cn网资源A.8065B.8064C.8063D.8062(第9题图)(第10题图)二、填空题.(每小题4分,共24分)11.如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=3,则点P到AB的距离是。第11题图第12题图第14题图12.如图所示,在△ABC中,∠B=90°,AB=3,AC=5,线段AC的垂直平分线DE交AC于D交BC于E。则△ABE的周长为.13.已知关于x的不等式(1-a)x>2的解集为x<,则a的取值范围是__________.14.如图,在等边△ABC中,AD=BE,BD、CE交于点P,CF⊥BD于F,若PF=3cm,则CP=cm.15.在不等式+a解集中有3个正整数,则a的取值范围是.16.如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为.三、解答题(一):(每小题6分,共18分)(第16题图)17.解不等式:2(x-1)≤10(x-3)-418.解不等式组23722)1(315xxxx(在数轴上表示解集)19.如图,在边长为1的小正方形组成的方格纸上,分别将网资源www.wang26....