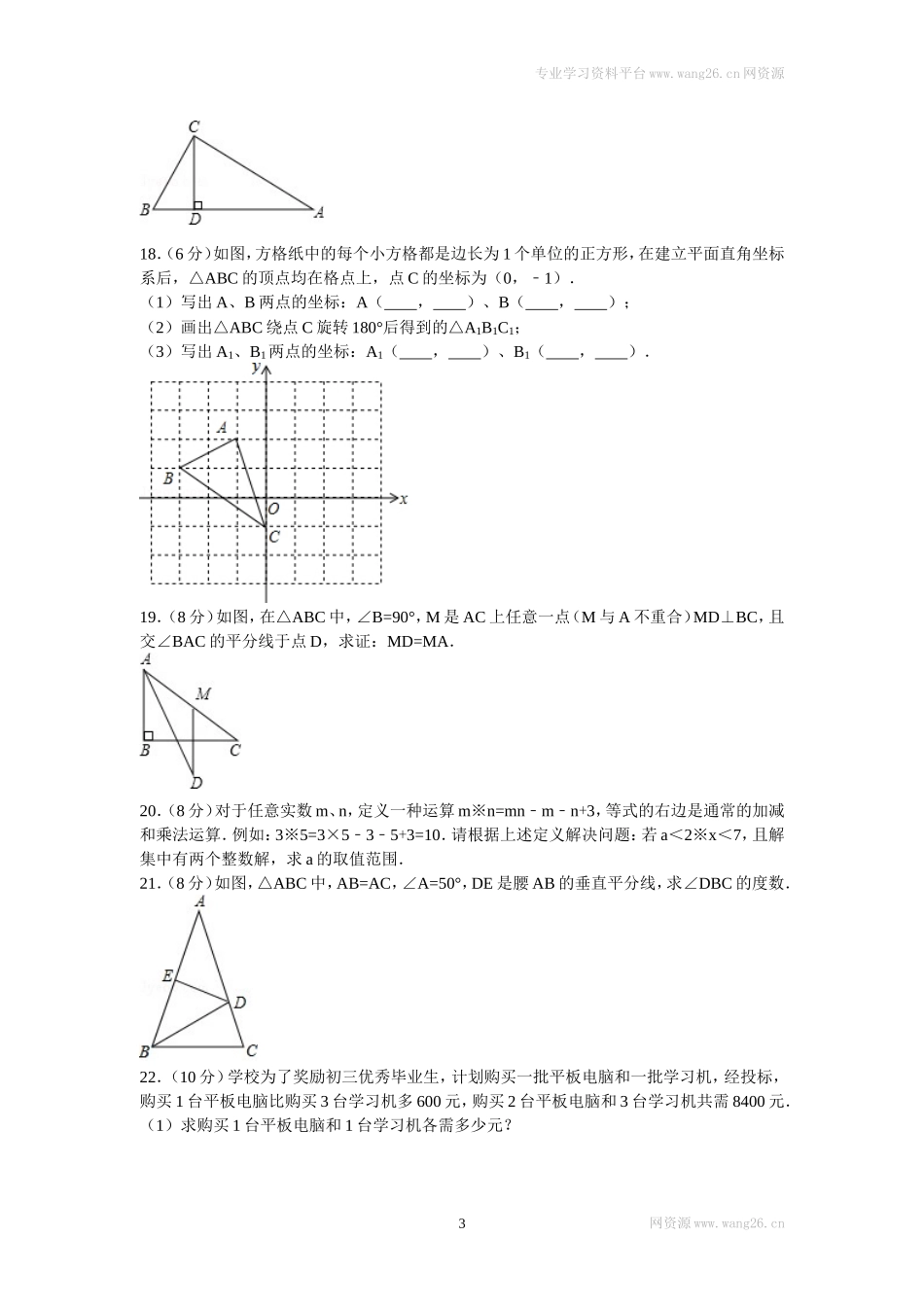
专业学习资料平台www.wang26.cn网资源2016年江西省萍乡市芦溪县八年级(下)期中数学试卷一、选择题(共6小题,每小题3分,满分18分)1.(3分)如图,数轴上所表示关于x的不等式组的解集是()A.x≥2B.x>2C.x>﹣1D.﹣1<x≤22.(3分)下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是()A.B.C.D.3.(3分)如图,在△ABC中,∠B=∠C,AB=5,则AC的长为()A.2B.3C.4D.54.(3分)点P(﹣2,﹣3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为()A.(﹣3,0)B.(﹣1,6)C.(﹣3,﹣6)D.(﹣1,0)5.(3分)如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为()A.30°B.45°C.90°D.135°6.(3分)如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有()A.3种B.6种C.8种D.12种二、填空题(共8小题,每小题3分,满分24分)7.(3分)用不等式表示:a+3大于﹣2:.网资源www.wang26.cn1专业学习资料平台www.wang26.cn网资源8.(3分)如果等腰三角形的一个底角是80°,那么顶角是度.9.(3分)不等式2x4﹣≥0的解集是.10.(3分)若直角三角形的一个锐角为50°,则另一个锐角的度数是度.11.(3分)如图,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ=°.12.(3分)如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.13.(3分)一次函数y=kx+b(k,b是常数,k≠0)图象如图所示,则不等式kx+b>0的解集是.14.(3分)如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=度.三、解答题(共8小题,满分58分)15.(6分)解不等式5x+15>0,并将解集在数轴上表示出来.16.(6分)解不等式组.17.(6分)如图,△ABC中,∠ACB=90°,CD是△ABC的高,∠A=30°,AB=4,求BD长.网资源www.wang26.cn2专业学习资料平台www.wang26.cn网资源18.(6分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,﹣1).(1)写出A、B两点的坐标:A(,)、B(,);(2)画出△ABC绕点C旋转180°后得到的△A1B1C1;(3)写出A1、B1两点的坐标:A1(,)、B1(,).19.(8分)...