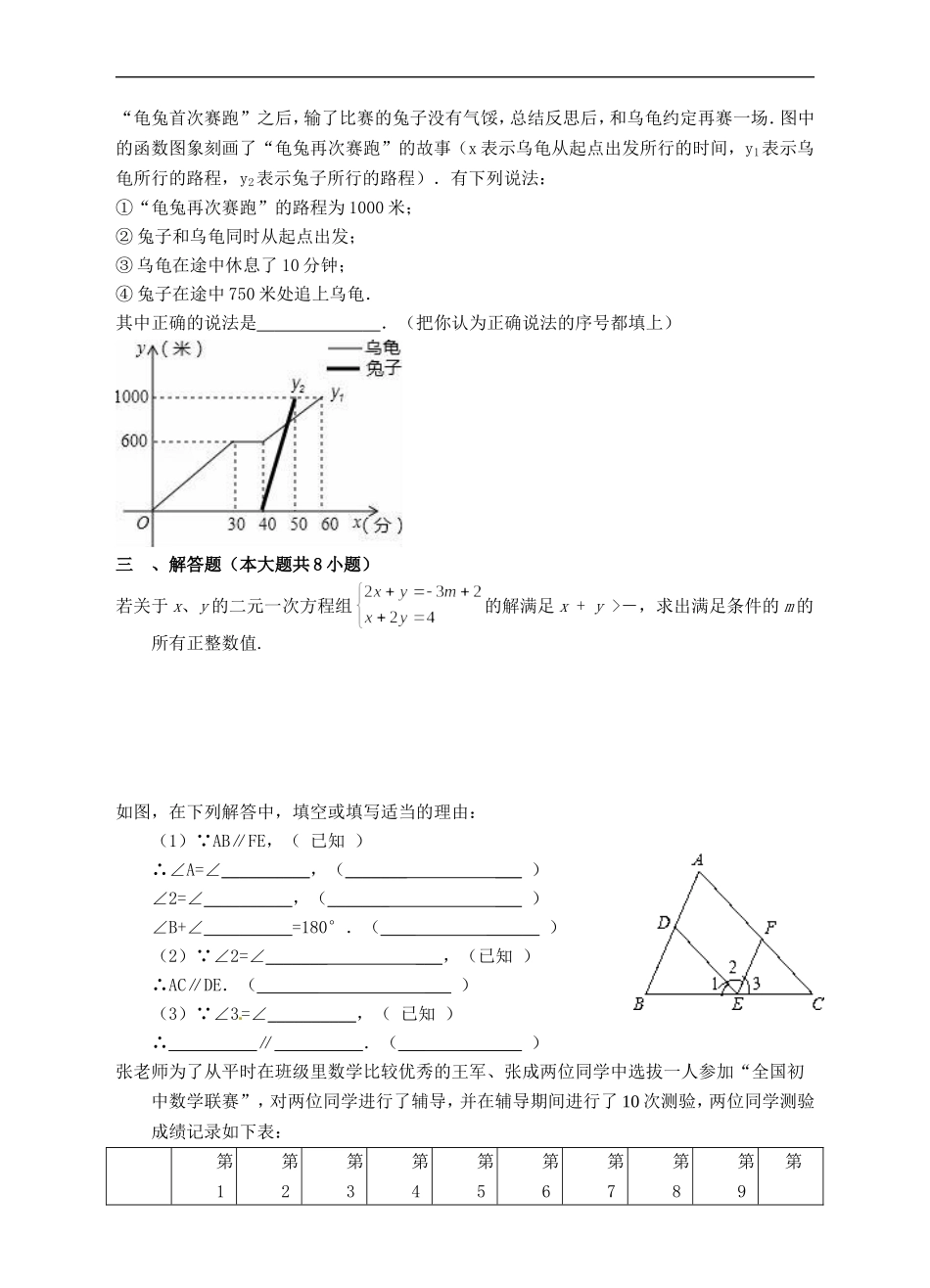
2016-2017北师大版八年级上数学期末模拟试题2姓名:__________班级:__________考号:__________一、选择题(本大题共12小题)的算术平方根是()A.2B.±2C.D.±下列四组数据中,不能作为直角三角形的三边长是()A.3,4,5B.3,5,7C.5,12,13D.6,8,10在实数0、π、、2+、3.12312312…、﹣、、1.1010010001…中,无理数的个数有()A.3个B.4个C.5个D.6个平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是()A.(3,﹣2)B.(2,3)C.(﹣2,﹣3)D.(2,﹣3)对于实数x、y,定义新运算:x※y=ax+by.其中a、b为常数,等式右边是通常的加法与乘法运算,已知1※(﹣2)=﹣3,2※3=8,则2010※(﹣2)的值为()A.2010B.2006C.2008D.2009一次函数y=2x﹣3的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限一组数据3、5、8、3、4的众数与中位数分别是()A.3,8B.3,3C.3,4D.4,3如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为()A.17°B.34°C.56°D.124°一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③不等式kx+b<x+a的解集为x<3中,正确的个数是()A.0B.1C.2D.3已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是()A.B.C.D.某商场购进商品后,加价40%作为销售价.商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元,两种商品原售价之和为490元,甲、乙两种商品的进价分别是()A.200元,150元B.210元,280元C.280元,210元D.150元,200元如图,直线233xy与x轴,y轴分别交于BA,两点,把AOB沿着直线AB翻折后得到BOA,则点O的坐标是()A.)3,3(B.)3,3(C.)32,2(D.)4,32(二、填空题(本大题共7小题)比较大小:25(填“>,<,=”).不等式>+2的解是.一组数据2,4,a,7,7的平均数=5,则方差S2=.方程组的解是如图是一次函数的y=kx+b图象,则关于x的不等式kx+b>0的解集为.若关于x,y的二元一次方程组的解满足x+y<2,则a的取值范围为__________.ABOO'xy“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;...