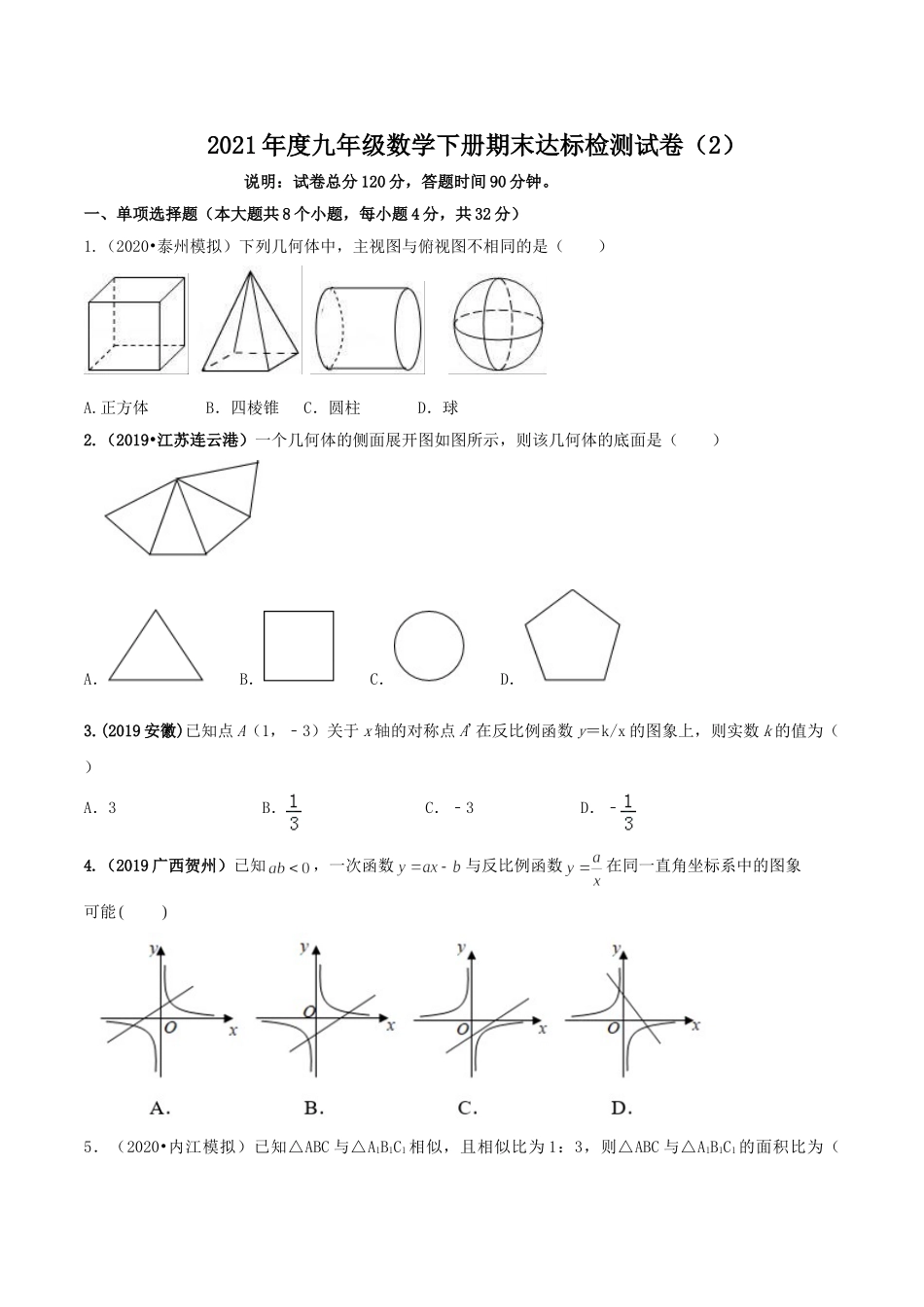
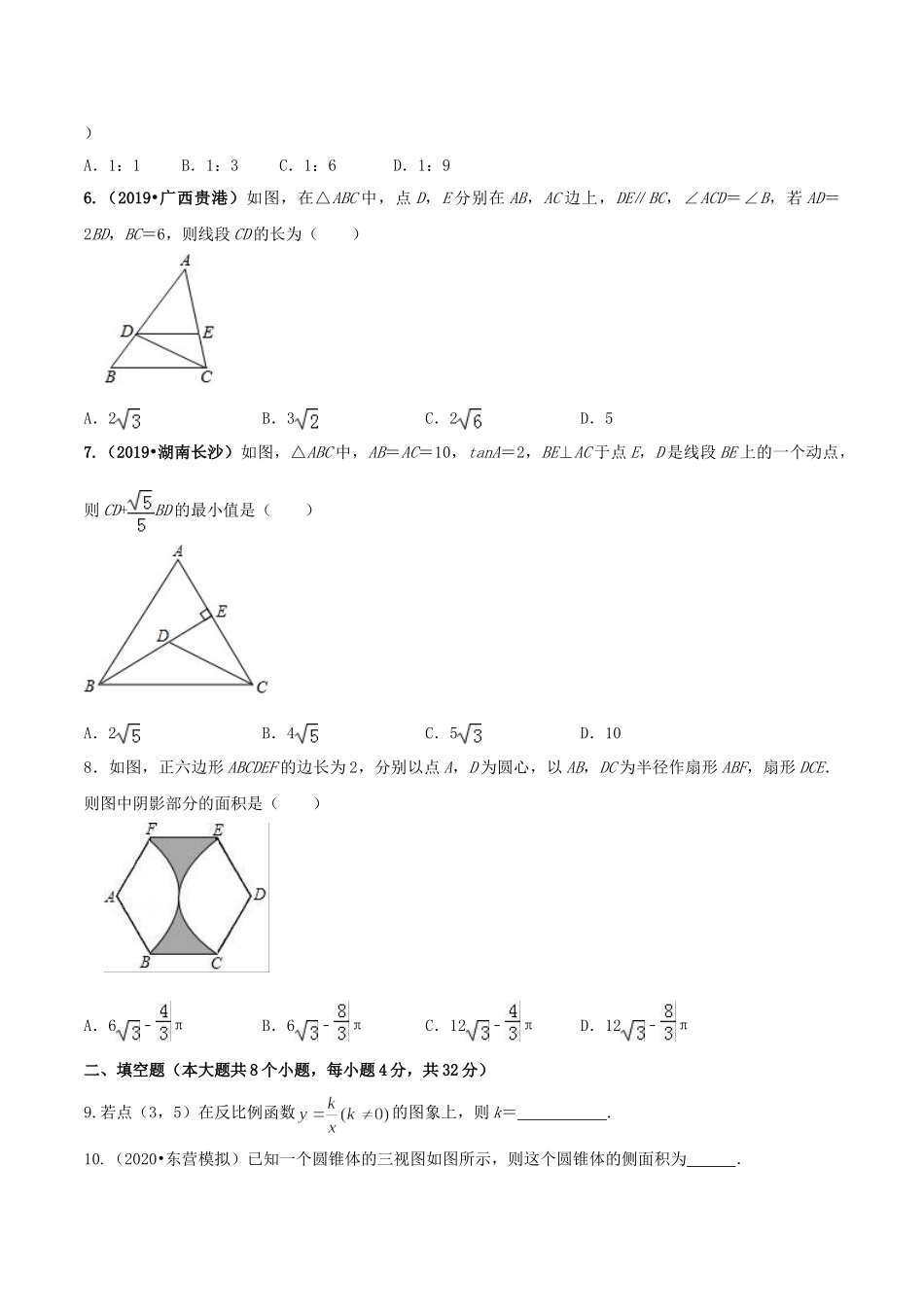
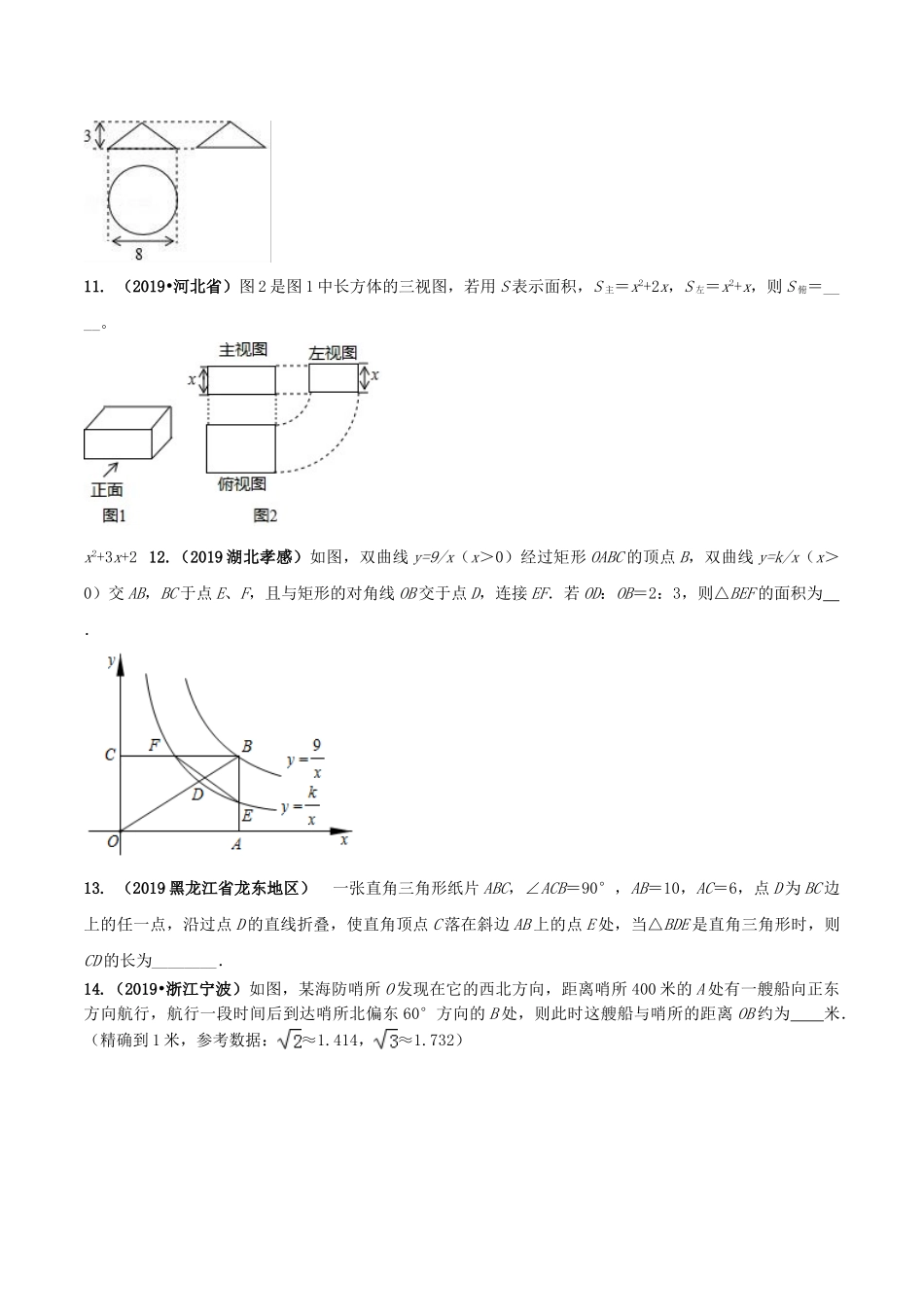
2021年度九年级数学下册期末达标检测试卷(2)说明:试卷总分120分,答题时间90分钟。一、单项选择题(本大题共8个小题,每小题4分,共32分)1.(2020•泰州模拟)下列几何体中,主视图与俯视图不相同的是()A.正方体B.四棱锥C.圆柱D.球2.(2019•江苏连云港)一个几何体的侧面展开图如图所示,则该几何体的底面是()A.B.C.D.3.(2019安徽)已知点A(1,﹣3)关于x轴的对称点A'在反比例函数y=k/x的图象上,则实数k的值为()A.3B.C.﹣3D.﹣4.(2019广西贺州)已知,一次函数与反比例函数在同一直角坐标系中的图象可能5.(2020•内江模拟)已知△ABC与△A1B1C1相似,且相似比为1:3,则△ABC与△A1B1C1的面积比为()A.1:1B.1:3C.1:6D.1:96.(2019•广西贵港)如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为()A.2B.3C.2D.57.(2019•湖南长沙)如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是()A.2B.4C.5D.108.如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF,扇形DCE.则图中阴影部分的面积是()A.6﹣πB.6﹣πC.12﹣πD.12﹣π二、填空题(本大题共8个小题,每小题4分,共32分)9.若点(3,5)在反比例函数的图象上,则k=.10.(2020•东营模拟)已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为.11.(2019•河北省)图2是图1中长方体的三视图,若用S表示面积,S主=x2+2x,S左=x2+x,则S俯=____。x2+3x+212.(2019湖北孝感)如图,双曲线y=9/x(x>0)经过矩形OABC的顶点B,双曲线y=k/x(x>0)交AB,BC于点E、F,且与矩形的对角线OB交于点D,连接EF.若OD:OB=2:3,则△BEF的面积为.13.(2019黑龙江省龙东地区)一张直角三角形纸片ABC,∠ACB=90°,AB=10,AC=6,点D为BC边上的任一点,沿过点D的直线折叠,使直角顶点C落在斜边AB上的点E处,当△BDE是直角三角形时,则CD的长为________.14.(2019•浙江宁波)如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为米.(精确到1米,参考数据:≈1.414,≈1.732)15.(2019•海南省)如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90...