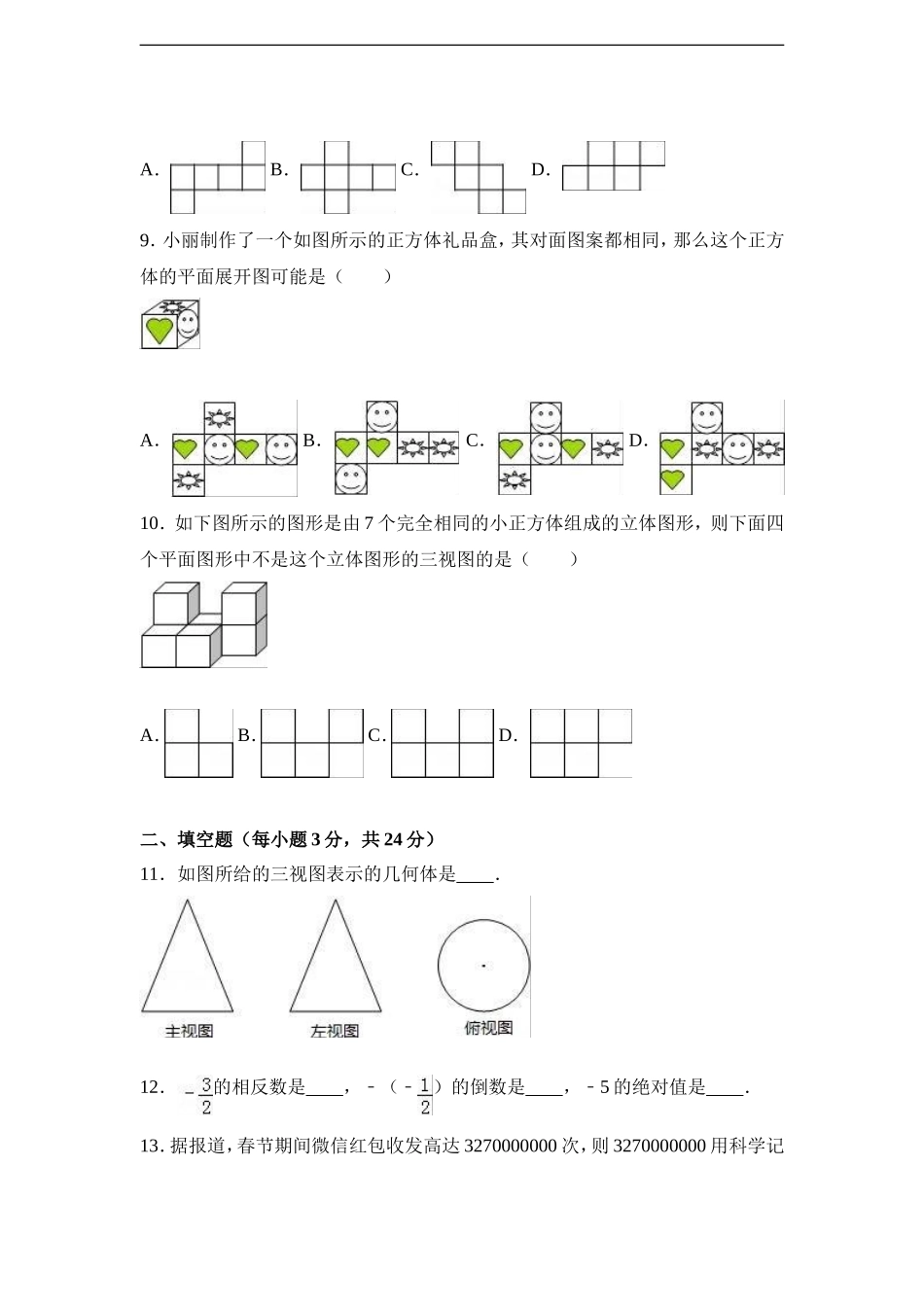
2016-2017学年云南省文山州富宁县洞波中学七年级(上)期中数学试卷一、选择题(每小题3分,共30分)1.如果收入200元记作+200元,那么支出150元记作()A.+150元B.﹣150元C.+50元D.﹣50元2.下列说法,其中正确的个数为()①正数和负数统称为有理数;②一个有理数不是整数就是分数;③有最小的负数,没有最大的正数;④符号相反的两个数互为相反数;⑤a﹣一定在原点的左边.A.1个B.2个C.3个D.4个3.数轴上有A,B,C,D四个点,其中绝对值相等的点是()A.点A与点DB.点A与点CC.点B与点CD.点B与点D4.﹣2016的相反数是()A.﹣2016B.2016C.±2016D.5.计算﹣32的结果是()A.9B.﹣9C.6D.﹣66.多项式2x2y35xy﹣23﹣的次数和项数分别是()A.5,3B.5,2C.8,3D.3,37.若单项式﹣3a5b与am+2b是同类项,则常数m的值为()A.﹣3B.4C.3D.28.以下各图均有彼此连接的六个小正方形纸片组成,其中不能折叠成一个正方体的是()A.B.C.D.9.小丽制作了一个如图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是()2-1-c-n-j-yA.B.C.D.10.如下图所示的图形是由7个完全相同的小正方体组成的立体图形,则下面四个平面图形中不是这个立体图形的三视图的是()A.B.C.D.二、填空题(每小题3分,共24分)11.如图所给的三视图表示的几何体是.12.的相反数是,﹣(﹣)的倒数是,﹣5的绝对值是.13.据报道,春节期间微信红包收发高达3270000000次,则3270000000用科学记数法表示为.www-2-1-cnjy-com14.已知(x2﹣)2+|3y2x﹣|=0,则x=,y=.15.用“>”,“<”,“=”填空:(1)0.70(2)﹣64(3)﹣.16.已知|x|=3,则x的值是.17.梯形的上底长为8,下底长为x,高是6,那么梯形面积y与下底长x之间的关系式是.18.如图是一组有规律的图案,图案1是由4个组成的,图案2是由7个组成的,那么图案5是由个组成的,依此,第n个图案是由个组成的.三、计算题(共28分)19.计算:(1)4592﹣+58﹣(2)(﹣+)×(﹣42)(3)2×(﹣5)+223﹣÷(4)﹣24+|610﹣|3﹣×(﹣1)2014.20.先化简,再求值:(1)3x4x﹣2+73x﹣+2x2+1,其中x=3﹣.(2)3x2y﹣[2x2y3﹣(2xyx﹣2y)﹣xy],其中x=1﹣,y=2﹣.四、解答题(21题5分,22题4分,23题6分,24题7分,25题8分,26题8分,共38分)21.(1)画出数轴,并用数轴上的点表示下列各数:5﹣,2.5,3,﹣,0,﹣3,3.(2)用“<”号把各数从小到...