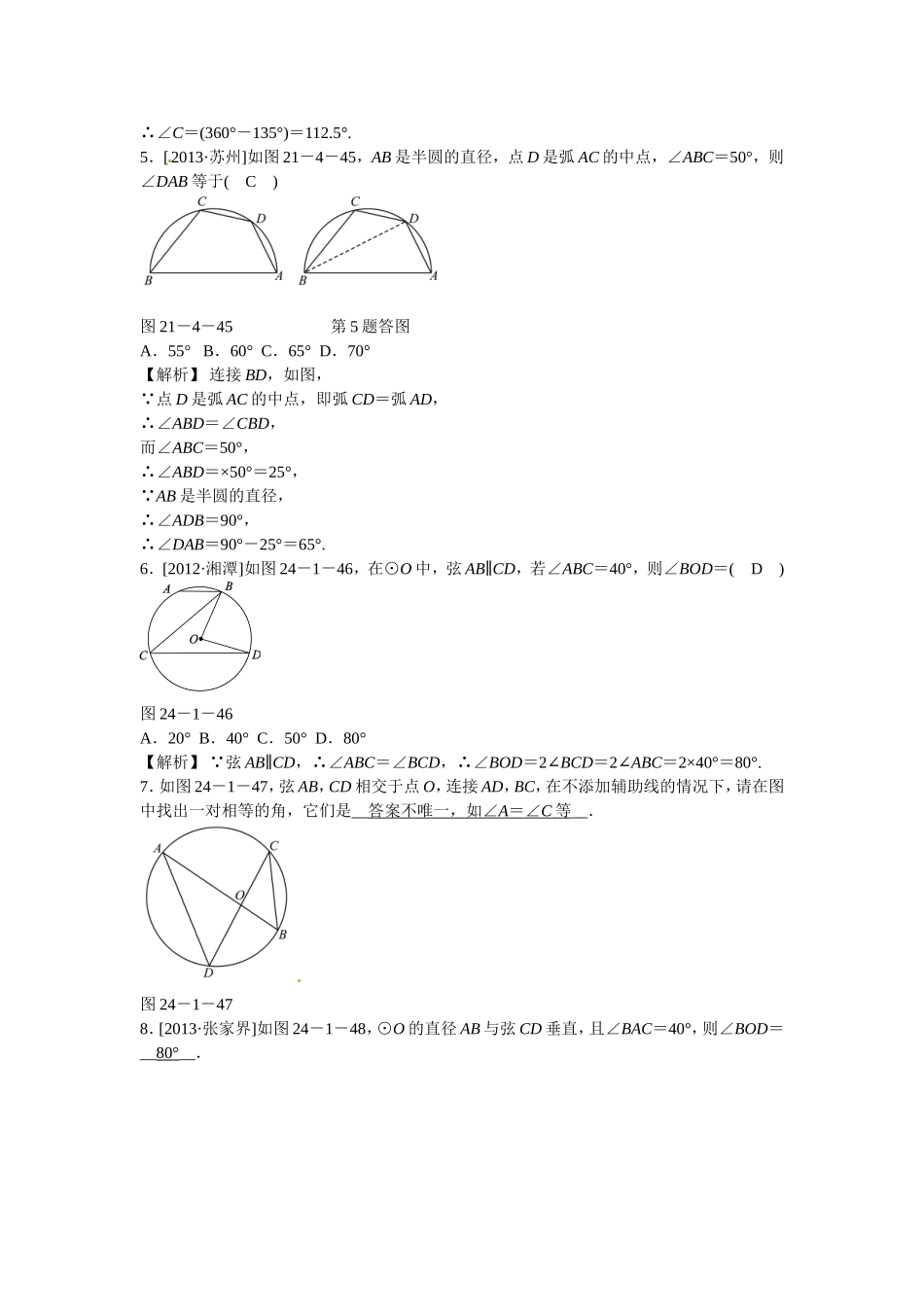
圆周角1.如图21-1-41,在⊙O中,∠ABC=50°,则∠AOC等于(D)图21-1-41A.50°B.80°C.90°D.100°2.如图21-1-42,点A,B,C在⊙O上,∠BOC=100°,则∠A的度数为(B)图21-1-42A.40°B.50°C.80°D.100°3.如图24-1-43,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=100°,则∠DCE的度数为(C)A.40°B.60°C.50°D.80°【解析】根据圆周角定理,可求得∠A的度数;由于四边形ABCD是⊙O的内接四边形,根据圆内接四边形的性质,可得∠DCE=∠A=50°.图24-1-434.如图21-4-44,在⊙O中,已知∠OAB=22.5°,则∠C的度数为(D)图21-4-44A.135°B.122.5°C.115.5°D.112.5°【解析】 OA=OB,∴∠OAB=∠OBC=22.5°,∴∠AOB=180°-22.5°-22.5°=135°.∴∠C=(360°-135°)=112.5°.5.[2013·苏州]如图21-4-45,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB等于(C)图21-4-45第5题答图A.55°B.60°C.65°D.70°【解析】连接BD,如图, 点D是弧AC的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°, AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°-25°=65°.6.[2012·湘潭]如图24-1-46,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=(D)图24-1-46A.20°B.40°C.50°D.80°【解析】 弦AB∥CD,∴∠ABC=∠BCD,∴∠BOD=2∠BCD=2∠ABC=2×40°=80°.7.如图24-1-47,弦AB,CD相交于点O,连接AD,BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是__答案不唯一,如∠A=∠C等__.图24-1-478.[2013·张家界]如图24-1-48,⊙O的直径AB与弦CD垂直,且∠BAC=40°,则∠BOD=__80°__.24-1-489.如图24-1-49,若AB是⊙O的直径,AB=10cm,∠CAB=30°,则BC=__5__cm.图24-1-4910.如图24-1-50,△ABC是⊙O的内接三角形,AB是⊙O的直径,点D为⊙O上的一点,若∠CAB=55°,则∠ADC的大小为__35__度.【解析】 AB为⊙O的直径,∴∠ACB=90°. ∠CAB=55°,∴∠B=90°-∠CAB=35°,∴∠ADC=∠B=35°.图24-1-5011.如图24-1-51,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为__30°__.【解析】因为AB为⊙O的直径,所以∠ADB=90°.又因为△ABC是等边三角形,所以AD是∠BAC的平分线,所以∠DAC=30°.图24-1-5112.如图24-1-52,在⊙O中,直径AB⊥CD于点E,...