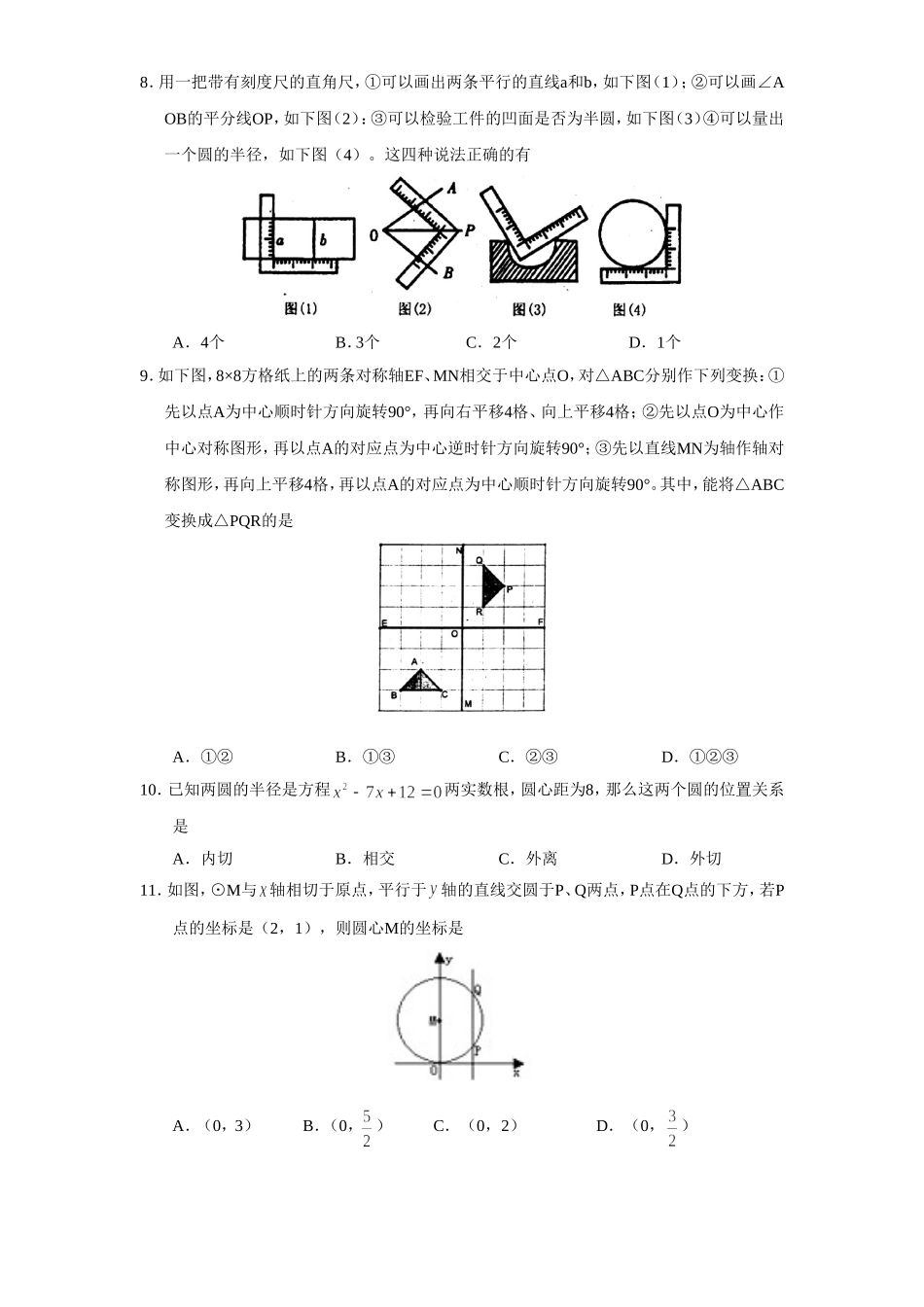
人教版九年级数学下册期末检测1附答案说明:本试题满分120分,考试时间120分钟。来源:www.bcjy123.com/tiku/一、选择题(下列各题的四个选项中,只有一项符合题意)1.在下列二次根式中,的取值范围是的是A.B.C.D.2.下列各式中是一元二次方程的是A.B.C.D.3.下列二次根式中属于最简二次根式的是A.B.C.D.4.化简的结果是A.B.C.0D.无法化简5.关于的一元二次方程的一个根为0,则的值为A.1B.-1C.1或-1D.6.下列平面图形中:既是轴对称图形,又是中心对称图形的是7.如下图,四边形PAOB是扇形OMN的内接矩形,顶点P在MN上,且不与M、N重合,当P点在MN上移动时,矩形PAOB的形状、大小随之变化,则AB的长度A.变大B.变小C.不变D.不能确定8.用一把带有刻度尺的直角尺,①可以画出两条平行的直线a和b,如下图(1);②可以画∠AOB的平分线OP,如下图(2):③可以检验工件的凹面是否为半圆,如下图(3)④可以量出一个圆的半径,如下图(4)。这四种说法正确的有A.4个B.3个C.2个D.1个9.如下图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,对△ABC分别作下列变换:①先以点A为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;②先以点O为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;③先以直线MN为轴作轴对称图形,再向上平移4格,再以点A的对应点为中心顺时针方向旋转90°。其中,能将△ABC变换成△PQR的是A.①②B.①③C.②③D.①②③10.已知两圆的半径是方程两实数根,圆心距为8,那么这两个圆的位置关系是A.内切B.相交C.外离D.外切11.如图,⊙M与轴相切于原点,平行于轴的直线交圆于P、Q两点,P点在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是A.(0,3)B.(0,)C.(0,2)D.(0,)12.如下图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动。那么()秒种后⊙P与直线CD相切。A.4B.8C.4或6D.4或8二、填空题(每小题3分,共18分)13.如果点A(-3,)是点B(3,-4)关于原点的对称点,那么等于__________。14.如下图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点。有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门。仅从射门角度考虑,应选择__________种射门方式。15.如下图,⊙O是△ABC内切...