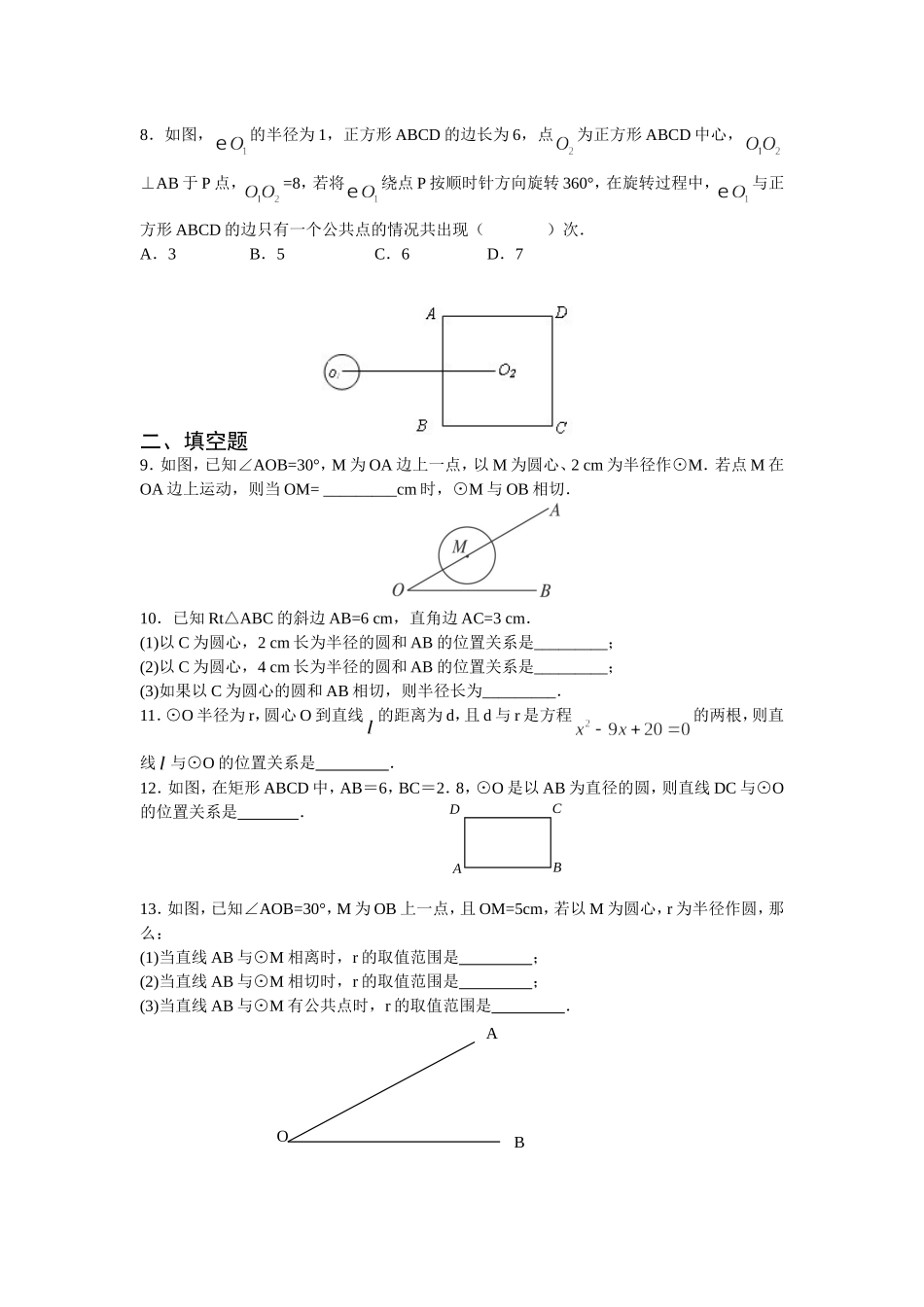
24.2.2直线和圆的位置关系(第一课时)知识点圆和圆的位置关系:1.直线和圆有三种位置关系:相交、相切、相离.相交:直线和圆_________________________,这时我们说这条直线和圆相交,这条直线叫做圆的割线,公共点叫做交点.相切:直线和圆_________________________,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.相离:直线和圆________________________,这时我们说这条直线和圆相离.2.设⊙O的半径为r,圆心O到直线的距离为d,那么:直线与⊙O相交dr.一、选择题1.已知⊙O的半径为8cm,若一条直线到圆心O的距离为8cm,那么这条直线和这个圆的位置关系是()A.相离B.相切C.相交D.相交或相离2.⊙O的半径r=5cm,点P在直线上,若OP=5cm,则直线l与⊙O的位置关系是()A.相离B.相切C.相交D.相切或相交3.已知⊙O的面积为9π,若点O到直线的距离为π,则直线与⊙O的位置关系是()A.相交B.相切C.相离D.无法确定4.设⊙O的半径为3,点O到直线的距离为d,若直线与⊙O至少有一个公共点,则d应满足的条件是()A.d=3B.d≤3C.d<3D.d>35.⊙O内最长弦长为m,直线与⊙O相离,设点O到的距离为d,则d与m的关系是()A.d=mB.d>mC.d>D.d<6.⊙O的半径为4,圆心O到直线的距离为,则直线与⊙O的位置关系是()A.相交B.相切C.相离D.无法确定7.如图,在平面直角坐标系中,⊙O的半径为1,则直线与⊙O的位置关系是()A.相离B.相切C.相交D.以上三种情况都有可能8.如图,的半径为1,正方形ABCD的边长为6,点为正方形ABCD中心,⊥AB于P点,=8,若将绕点P按顺时针方向旋转360°,在旋转过程中,与正方形ABCD的边只有一个公共点的情况共出现()次.A.3B.5C.6D.7二、填空题9.如图,已知∠AOB=30°,M为OA边上一点,以M为圆心、2cm为半径作⊙M.若点M在OA边上运动,则当OM=_________cm时,⊙M与OB相切.10.已知Rt△ABC的斜边AB=6cm,直角边AC=3cm.(1)以C为圆心,2cm长为半径的圆和AB的位置关系是_________;(2)以C为圆心,4cm长为半径的圆和AB的位置关系是_________;(3)如果以C为圆心的圆和AB相切,则半径长为_________.11.⊙O半径为r,圆心O到直线的距离为d,且d与r是方程的两根,则直线与⊙O的位置关系是.12.如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是.13.如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,若以M...