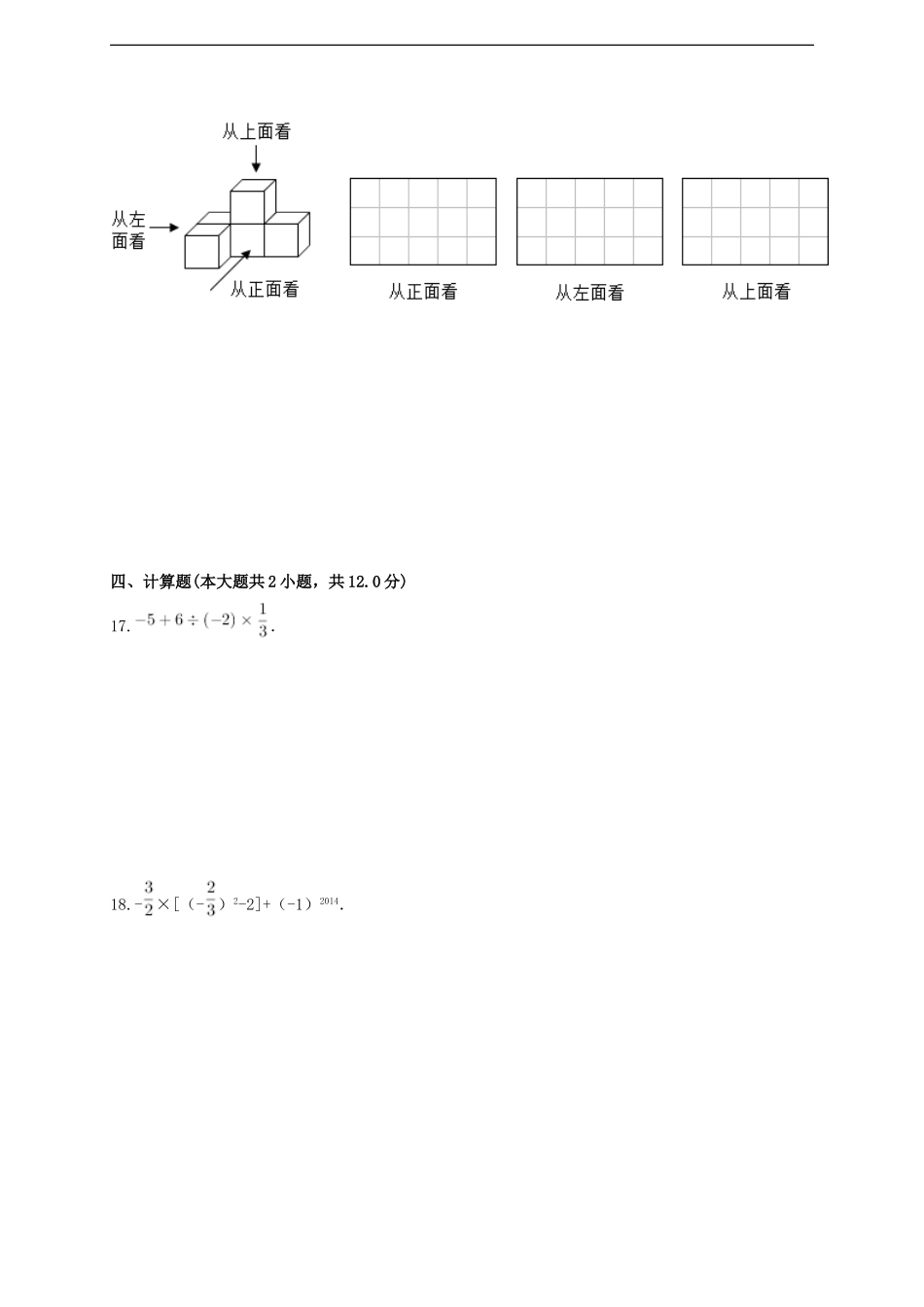
江西省抚州市临川区第十中学2016-2017学年七年级数学上学期期中试题一、填空题(本大题共8小题,共24.0分)1.-0.5的绝对值是______,相反数是______,倒数是______.2.从数-6,1,-3,5,-2中任取二个数相乘,其积最小的是______.3.某天的最高气温为8℃,最低气温为-2℃,则这天的温差是______℃.4.化简:3x-2(x-3y)=______.5.在数轴上,与表示-2的点距离为5个单位的点表示的数是______.6.若单项式-2xmy3与3x2yn是同类项,则mn的值是______.7.如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出输出的结果为12,…则第2014次输出的结果为______.www.21-cn-jy.com8.如图是一个正方体的展开图,和C面的对面是______面.二、选择题(本大题共6小题,共18.0分)9.在有理数-3,-(-3),-|-3|,-32,(-3)2,(-3)3,﹢(-3),-33中负数的个数是()A.4B.5C.6D.72·1·c·n·j·y10.绝对值不大于3的所有整数的和是()A.0B.-1C.1D.6【来源:21·世纪·教育·网】11.若多项式x2-3kxy-3y2+9xy-8中不含xy项,则k等于()A.0B.3C.19D.-192-1-c-n-j-y12.若|a|=3,|b|=5,a与b异号,则|a-b|的值为()A.2B.-2C.8D.2或821·世纪*教育网13.根据2010年第六次全国人口普查主要数据公报,广东省常住人口约为10430万人.这个数据可以用科学记数法表示为()A.1.043×108人B.1.043×107人C.1.043×104人D.1043×105人21*cnjy*com14.如图,边长为(m+3)的正方形纸片,剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是()A.m+3B.m+6C.2m+3D.2m+6【来源:21cnj*y.co*m】三、解答题(本大题共2小题,共12.0分)15.将下列各数在数轴上表示出来,并用“<”连接:-22,-(-1),0,|-3|,-2.5.【出处:21教育名师】16.从正面、左面、上面观察如图1所示的几何体,分别在图2中画出你所看到的几何体的形状图.【版权所有:21教育】四、计算题(本大题共2小题,共12.0分)17..18.-×[(-)2-2]+(-1)2014.五、解答题(本大题共2小题,共12.0分)19.x+(2x-1)-(5x+4)20.(x3+xy2)-2(x3y-2xy2)六、计算题(本大题共2小题,共15.0分)21.已知|3a+6|+(1-b)2=0,求2a2-4ab+b2与-3a2+2ab-5b2的差.21cnjy.com22.小明早晨跑步,他从自家向东跑了2千米到达小彬家,继续向东跑了1.5千米到达小红家,然后向西跑了4.5千米到达中心广场,最后回到家.(1)以小明家为原点,以...