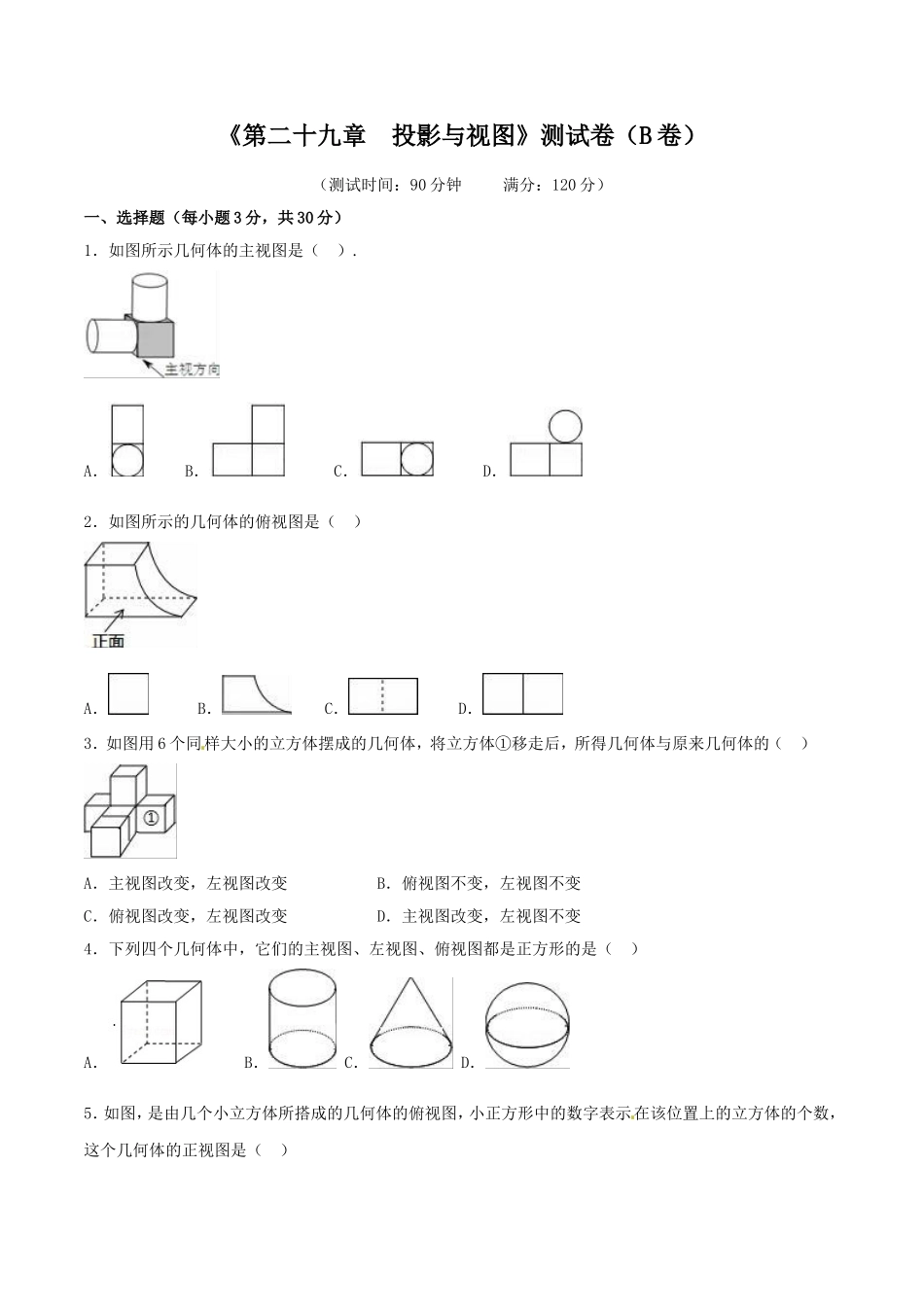
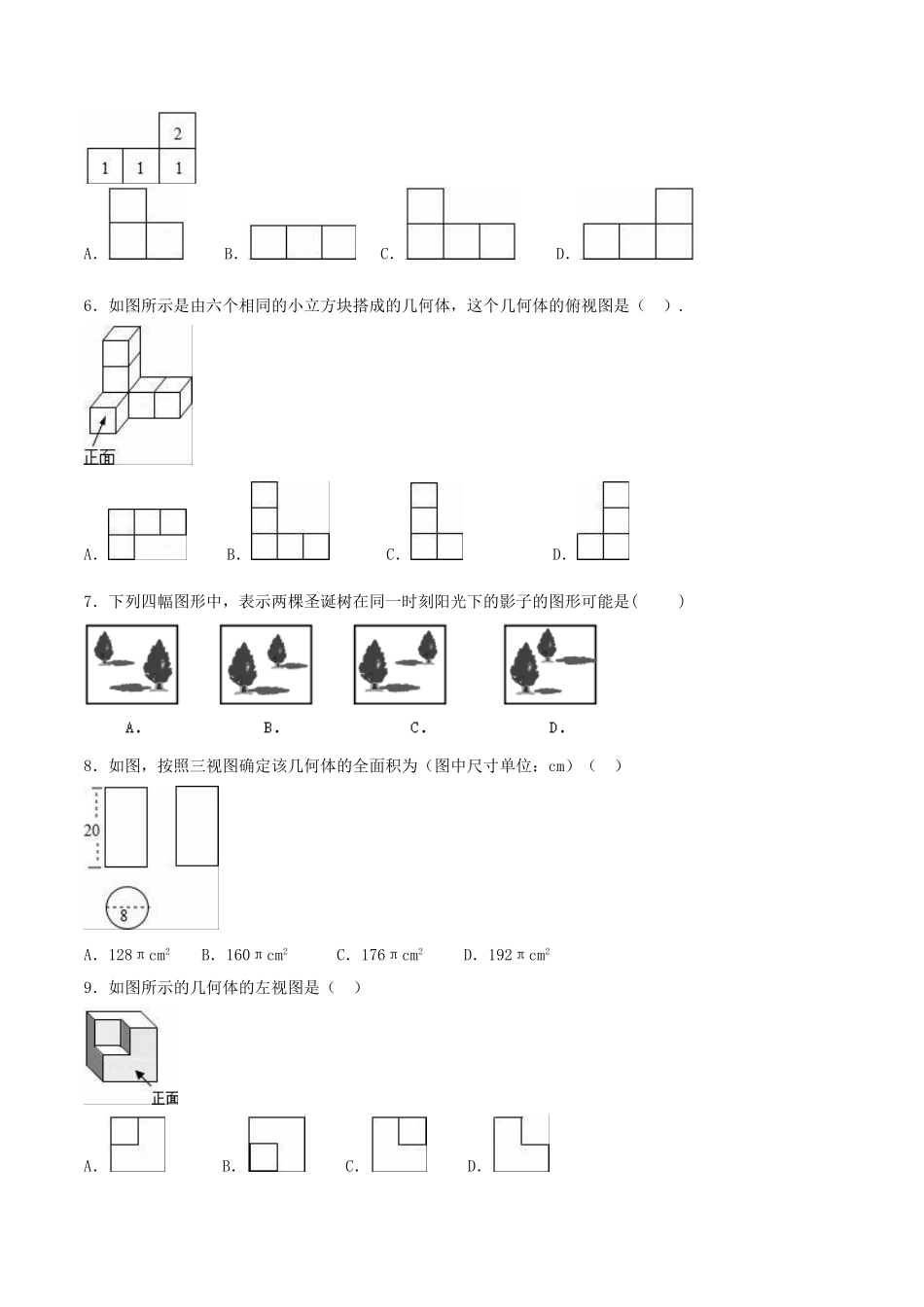
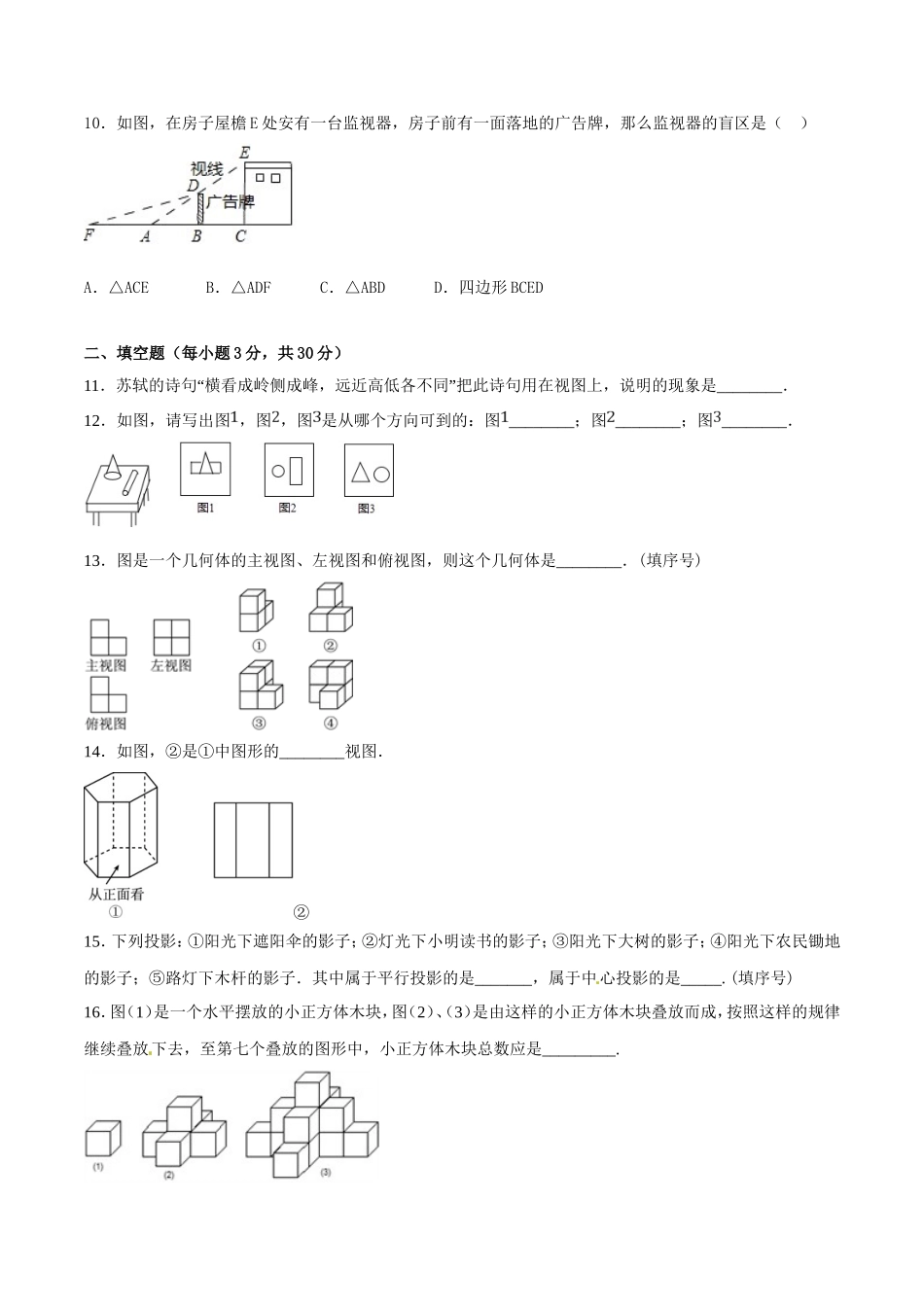
《第二十九章投影与视图》测试卷(B卷)(测试时间:90分钟满分:120分)一、选择题(每小题3分,共30分)1.如图所示几何体的主视图是().A.B.C.D.2.如图所示的几何体的俯视图是()[来源:学&科&网Z&X&X&K]A.B.C.D.3.如图用6个同样大小的立方体摆成的几何体,将立方体①移走后,所得几何体与原来几何体的()[来源:学科网ZXXK]A.主视图改变,左视图改变B.俯视图不变,左视图不变C.俯视图改变,左视图改变D.主视图改变,左视图不变4.下列四个几何体中,它们的主视图、左视图、俯视图都是正方形的是()A.B.C.D.5.如图,是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的立方体的个数,这个几何体的正视图是()[来源:学科网]A.B.C.D.6.如图所示是由六个相同的小立方块搭成的几何体,这个几何体的俯视图是().A.B.C.D.7.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是()8.如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)()A.128πcm2B.160πcm2C.176πcm2D.192πcm29.如图所示的几何体的左视图是()A.B.C.D.10.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是()A.△ACEB.△ADFC.△ABDD.四边形BCED二、填空题(每小题3分,共30分)11.苏轼的诗句“横看成岭侧成峰,远近高低各不同”把此诗句用在视图上,说明的现象是________.12.如图,请写出图,图,图是从哪个方向可到的:图________;图________;图________.13.图是一个几何体的主视图、左视图和俯视图,则这个几何体是________.(填序号)14.如图,②是①中图形的________视图.②15.下列投影:①阳光下遮阳伞的影子;②灯光下小明读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子.其中属于平行投影的是_______,属于中心投影的是_____.(填序号)16.图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是_________.17.有两根大小、形状完全相同的铁丝,甲铁丝与投影面的夹角是45°,乙铁丝与投影面的夹角是30°,那么两根铁丝在投影面的正投影的长度的大小关系是:甲____乙(填“>”“<”或“=”).18.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,那么线段AC在AB上的正投影是___,线段CD在AB上的...