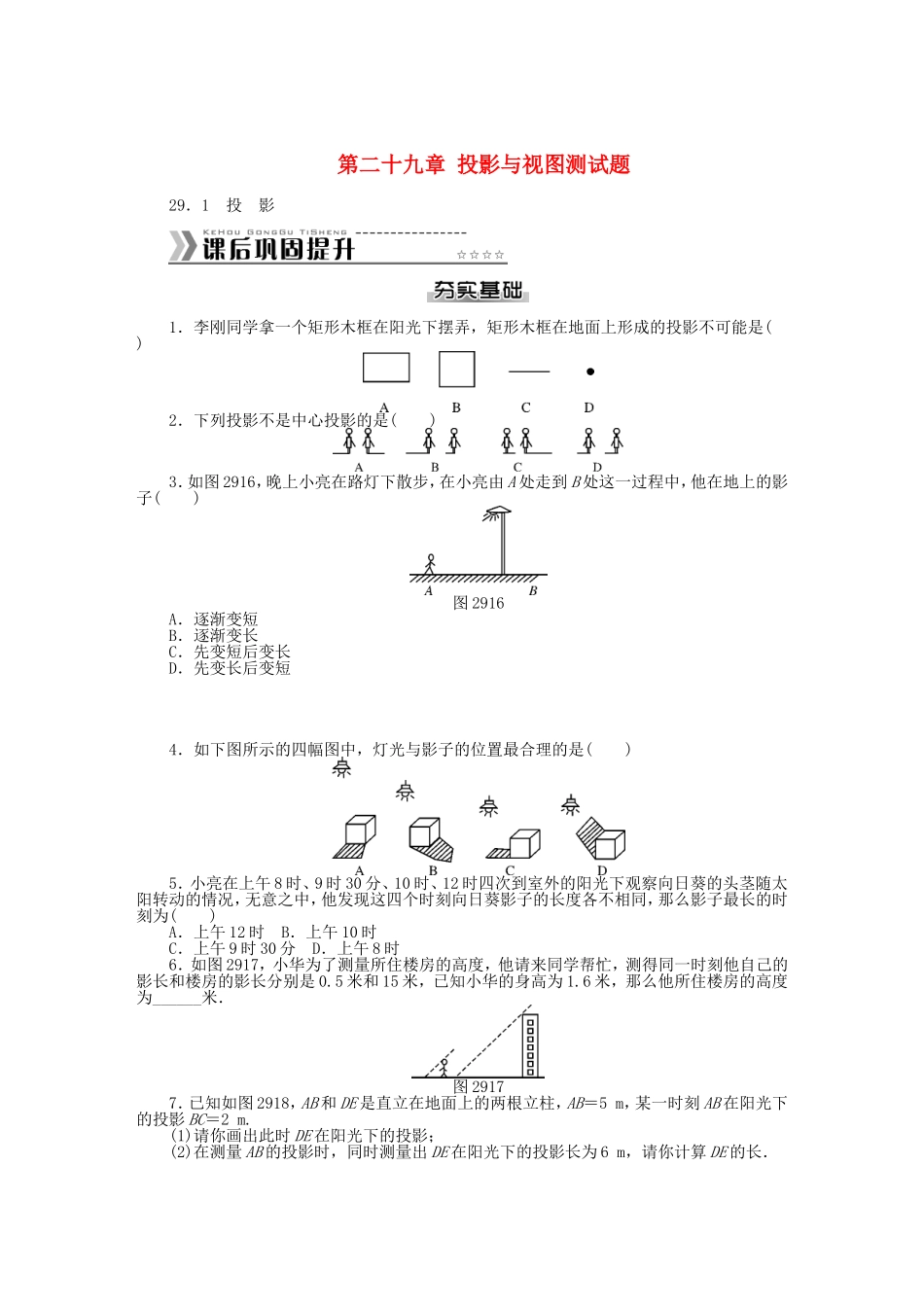
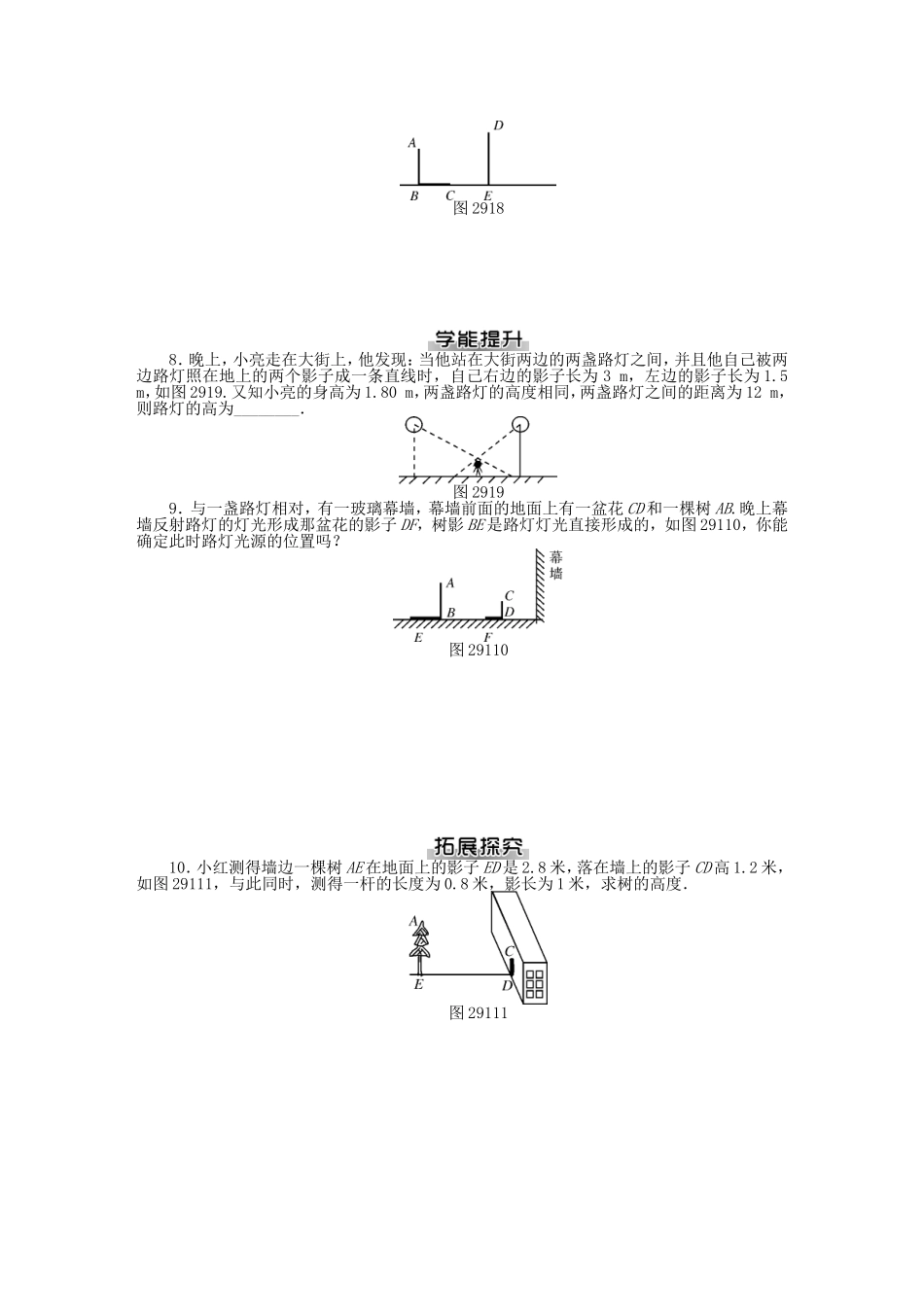
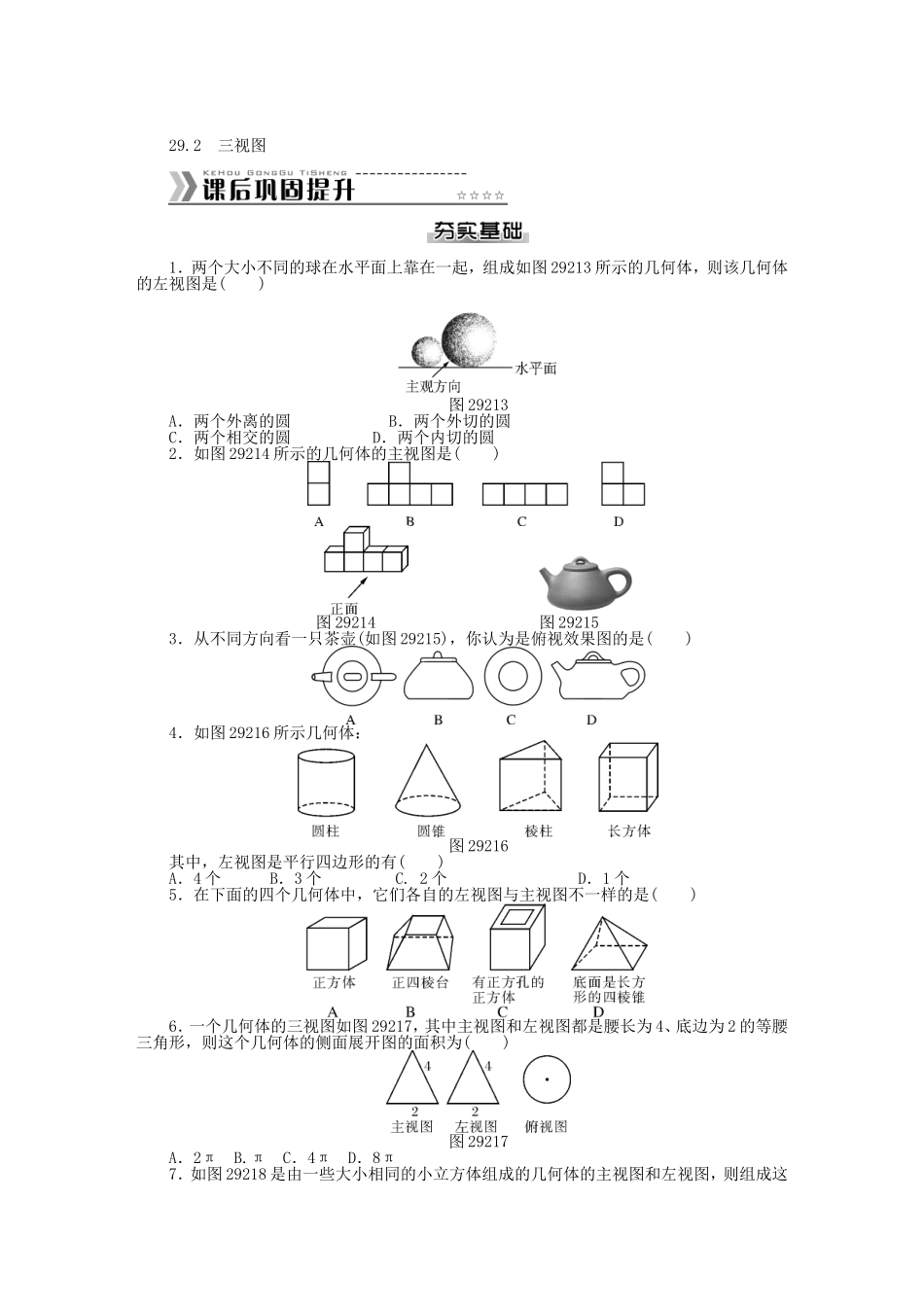
第二十九章投影与视图测试题29.1投影1.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是()2.下列投影不是中心投影的是()3.如图2916,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子()图2916A.逐渐变短B.逐渐变长C.先变短后变长D.先变长后变短4.如下图所示的四幅图中,灯光与影子的位置最合理的是()5.小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为()A.上午12时B.上午10时C.上午9时30分D.上午8时6.如图2917,小华为了测量所住楼房的高度,他请来同学帮忙,测得同一时刻他自己的影长和楼房的影长分别是0.5米和15米,已知小华的身高为1.6米,那么他所住楼房的高度为______米.图29177.已知如图2918,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.(1)请你画出此时DE在阳光下的投影;(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.图29188.晚上,小亮走在大街上,他发现:当他站在大街两边的两盏路灯之间,并且他自己被两边路灯照在地上的两个影子成一条直线时,自己右边的影子长为3m,左边的影子长为1.5m,如图2919.又知小亮的身高为1.80m,两盏路灯的高度相同,两盏路灯之间的距离为12m,则路灯的高为________.图29199.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花CD和一棵树AB.晚上幕墙反射路灯的灯光形成那盆花的影子DF,树影BE是路灯灯光直接形成的,如图29110,你能确定此时路灯光源的位置吗?图2911010.小红测得墙边一棵树AE在地面上的影子ED是2.8米,落在墙上的影子CD高1.2米,如图29111,与此同时,测得一杆的长度为0.8米,影长为1米,求树的高度.图2911129.2三视图1.两个大小不同的球在水平面上靠在一起,组成如图29213所示的几何体,则该几何体的左视图是()图29213A.两个外离的圆B.两个外切的圆C.两个相交的圆D.两个内切的圆2.如图29214所示的几何体的主视图是()图29214图292153.从不同方向看一只茶壶(如图29215),你认为是俯视效果图的是()4.如图29216所示几何体:图29216其中,左视图是平行四边形的有()A.4个B.3个C.2个D.1个5.在下面的四个几何体中,它们各自的左视图与主视图不一样的是()6.一个几何体的三视图如图29217,其中主视图和左视图都是腰长为4、底...