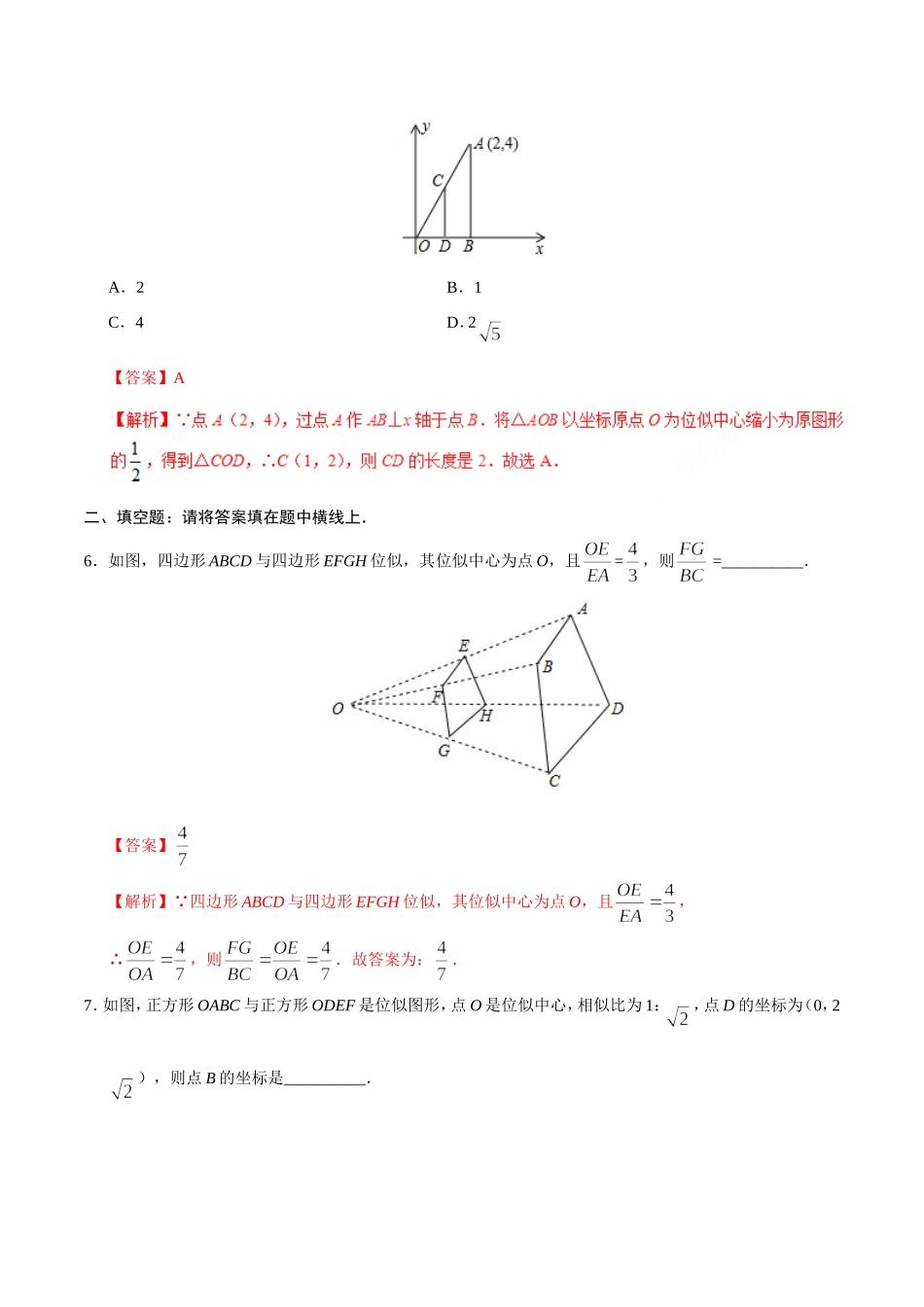
第二十七章相似27.3位似一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,在正方形网格中,△ABC和△DEF相似,则关于位似中心与相似比叙述正确的是A.位似中心是点B,相似比是2:1B.位似中心是点D,相似比是2:1C.位似中心在点G,H之间,相似比为2:1D.位似中心在点G,H之间,相似比为1:2【答案】C【解析】如图,在正方形网格中,△ABC和△DEF相似,连接AF,CE,∴位似中心在点G,H之间,又 AC=2EF,∴相似比为2:1,故选C.2.在平面直角坐标系中,点A(–6,2),B(–4,–4),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是A.(–3,1)B.(–12,4)C.(–12,4)或(12,–4)D.(–3,1)或(3,–1)【答案】D【解析】 △ABC的一个顶点A的坐标是(–6,2),以原点O为位似中心相似比为1:2将△ABC缩小得到它的位似图形△A′B′C′,∴点A′的坐标是:(–×6,×2)或(–×(–6),–×2),即点A′的坐标为(–3,1)或(3,–1).故选D.3.如图,已知△A1OB1与△A2OB2位似,且△A1OB1与△A2OB2的周长之比为1:2,点A1的坐标为(–1,2),则点A2的坐标为A.(1,–4)B.(2,–4)C.(–4,2)D.(–,1)【答案】B【解析】 △A1OB1与△A2OB2的周长之比为1:2,∴△A1OB1与△A2OB2的位似之比为1:2,而点A1的坐标为(–1,2),∴点A2的坐标为(2,–4).故选B.4.如图,在6×6网格图中,每个小正方形的边长均为1,则关于三角形①、②的下列四个说法中正确的是A.一定不相似B.一定位似C.一定相似,且相似比为1:2D.一定相似,且相似比为1:4【答案】C【解析】由已知图形可得:三角形①、②一定相似,且相似比为1:2.故选C.5.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,则CD的长度是A.2B.1C.4D.2【答案】A二、填空题:请将答案填在题中横线上.6.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=__________.【答案】【解析】 四边形ABCD与四边形EFGH位似,其位似中心为点O,且,∴,则.故答案为:.7.如图,正方形OABC与正方形ODEF是位似图形,点O是位似中心,相似比为1:,点D的坐标为(0,2),则点B的坐标是__________.【答案】(2,2)【解析】 正方形OABC与正方形ODEF是位似图形,点O是位似中心,相似比为1:,点D的坐标为(0,2),∴DE=...