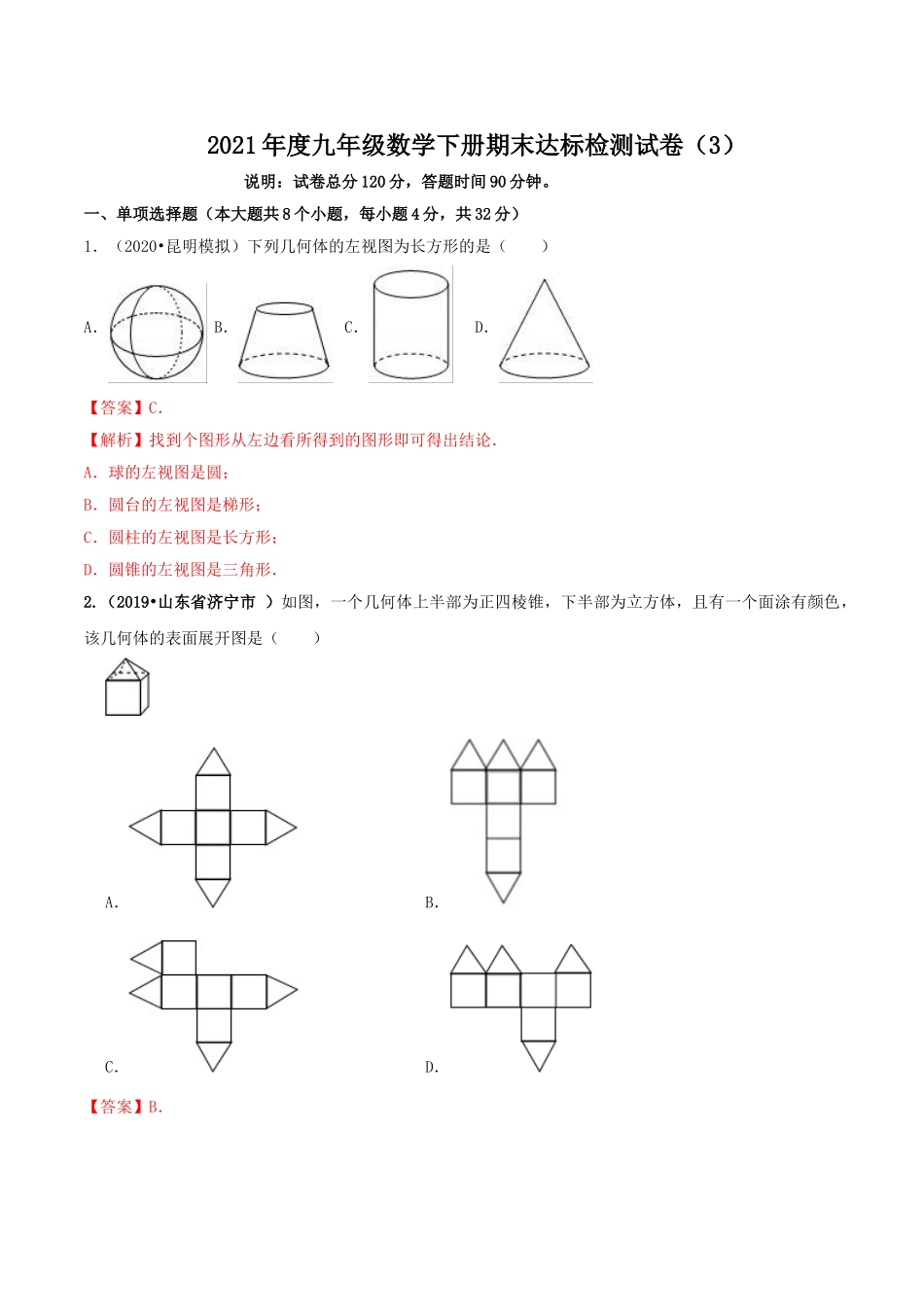
2021年度九年级数学下册期末达标检测试卷(3)说明:试卷总分120分,答题时间90分钟。一、单项选择题(本大题共8个小题,每小题4分,共32分)1.(2020•昆明模拟)下列几何体的左视图为长方形的是()A.B.C.D.【答案】C.【解析】找到个图形从左边看所得到的图形即可得出结论.A.球的左视图是圆;B.圆台的左视图是梯形;C.圆柱的左视图是长方形;D.圆锥的左视图是三角形.2.(2019•山东省济宁市)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是()A.B.C.D.【答案】B.【解析】考点是几何体的展开图。由平面图形的折叠及几何体的展开图解题,注意带图案的一个面不是底面.本题主要考查了几何体的展开图.解题时勿忘记正四棱柱的特征及正方体展开图的各种情形.注意做题时可亲自动手操作一下,增强空间想象能力.选项A和C带图案的一个面是底面,不能折叠成原几何体的形式;选项B能折叠成原几何体的形式;选项D折叠后下面带三角形的面与原几何体中的位置不同.3.(2019黑龙江哈尔滨)点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()。A.(4,-1)B.(-,1)C.(-4,-1)D.(,2)【答案】A【解析】反比例函数的图象及性质将点(﹣1,4)代入y=,∴k=﹣4,∴y=,∴点(4,﹣1)在函数图象上。4.(2019•湖南衡阳)如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m为常数且m≠0)的图象都经过A(﹣1,2),B(2,﹣1),结合图象,则不等式kx+b>的解集是()A.x<﹣1B.﹣1<x<0C.x<﹣1或0<x<2D.﹣1<x<0或x>2【答案】C.【解析】根据一次函数图象在反比例函数图象上方的x的取值范围便是不等式kx+b>的解集.由函数图象可知,当一次函数y1=kx+b(k≠0)的图象在反比例函数y2=(m为常数且m≠0)的图象上方时,x的取值范围是:x<﹣1或0<x<2,∴不等式kx+b>的解集是x<﹣1或0<x<25.(2019▪湖北黄石)如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于点A,反比例函数y=(x>0)的图象与线段AB相交于点C,且C是线段AB的中点,点C关于直线y=x的对称点C'的坐标为(1,n)(n≠1),若△OAB的面积为3,则k的值为()A.B.1C.2D.3【答案】D.【解析】根据对称性求出C点坐标,进而得OA与AB的长度,再根据已知三角形的面积列出n的方程求得n,进而用待定系数法求得k. 点C关于直线y=x的对称点C'的坐标为(1,n)(n≠1),∴C(...